Предмет: Алгебра,
автор: Карина996K
Найти производную. Помогите пожалуйста
Приложения:
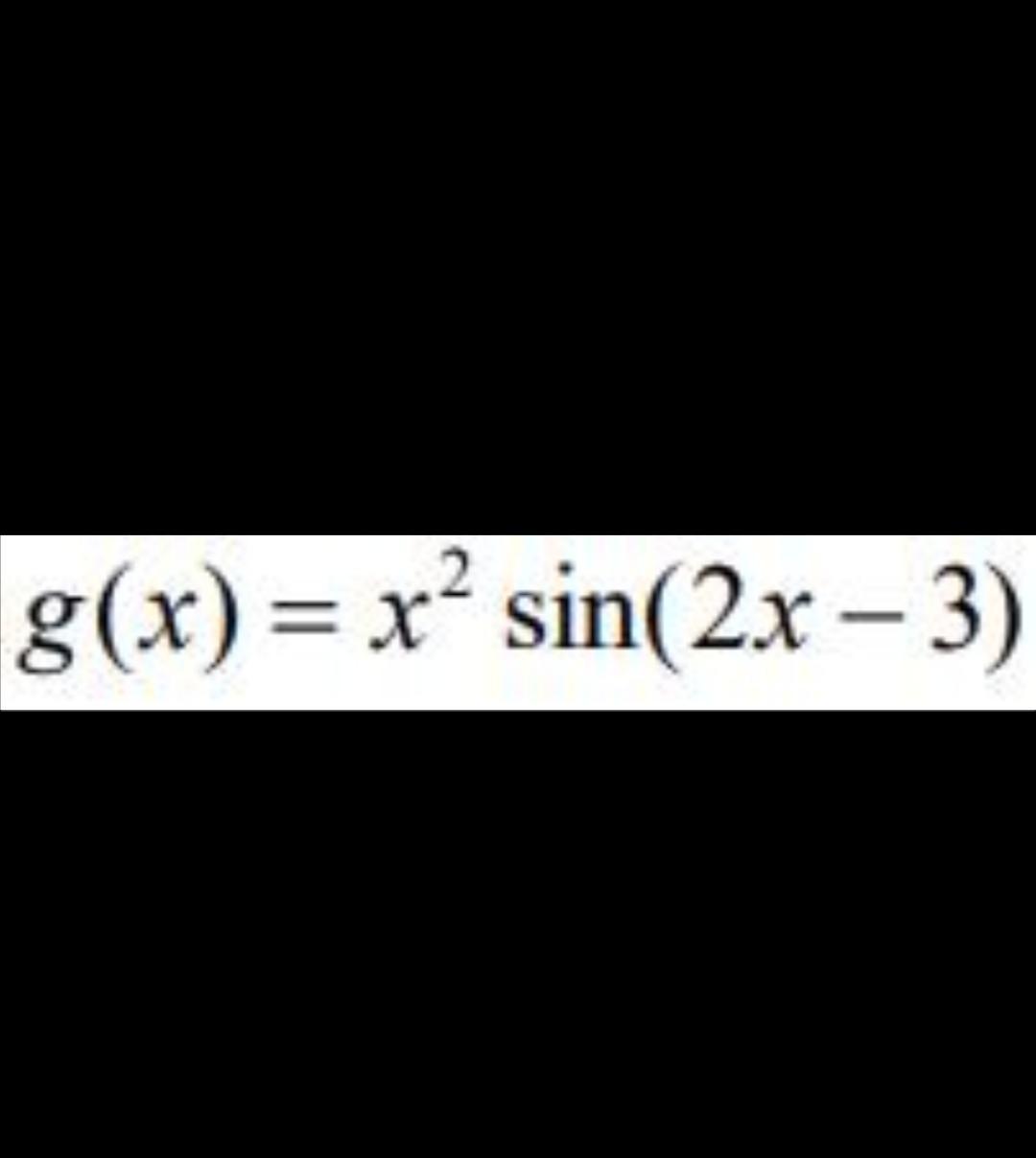
Ответы
Автор ответа:
1
Ответ:
Объяснение:
Правила дифференцирования, которые понадобились в этом задании
Кусок таблицы производных, который понадобился в данном заданий
Похожие вопросы
Предмет: Қазақ тiлi,
автор: monti12
Предмет: Русский язык,
автор: wakalarwakslag
Предмет: Немецкий язык,
автор: 34tanka
Предмет: Математика,
автор: Dоubl
Предмет: Математика,
автор: Moonspellpasha