Предмет: Математика,
автор: politerhon
Здравствуйте !
Меня интересует способ решения неравенств такого характера:

и

Ответы
Автор ответа:
1
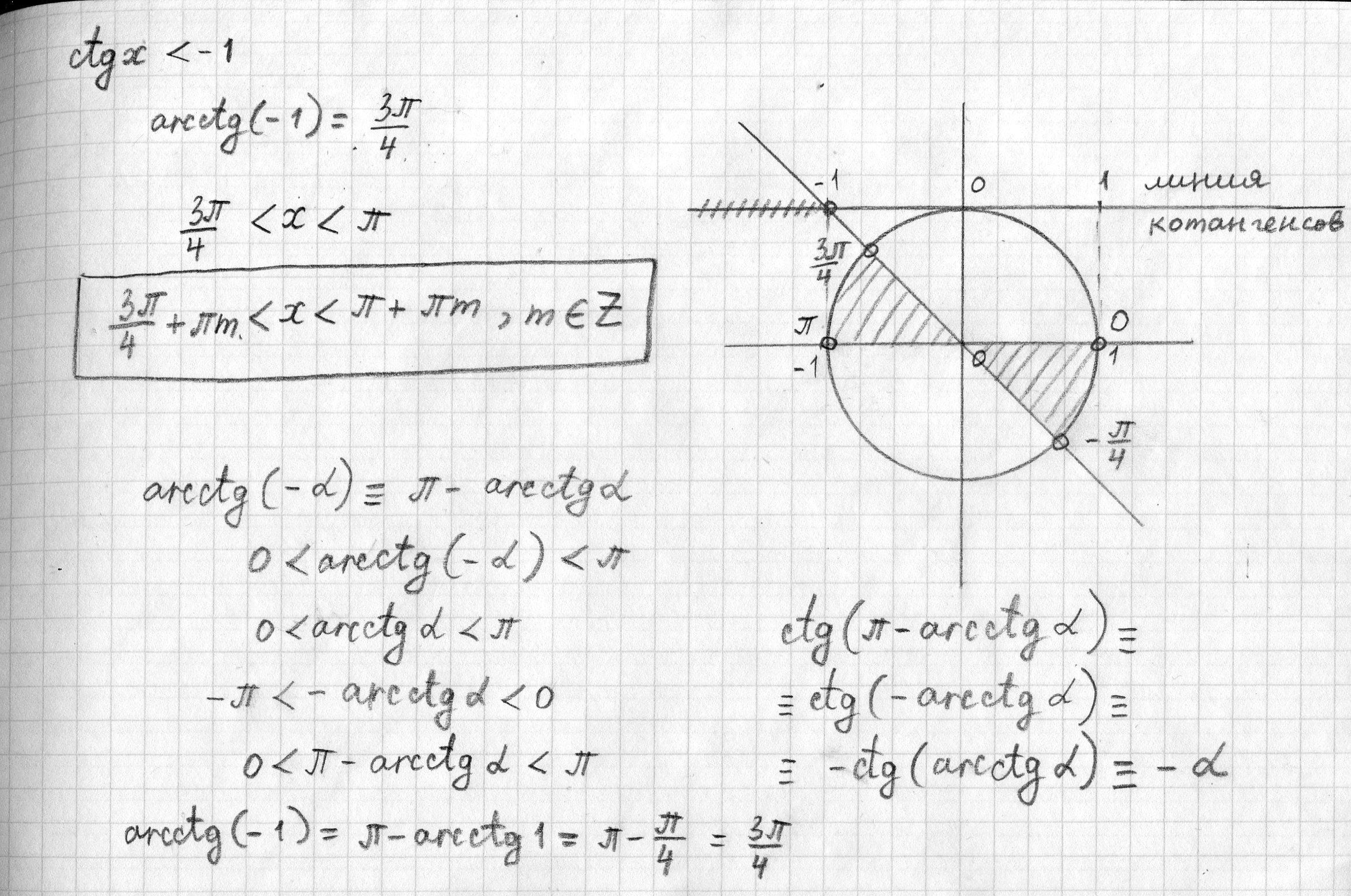
я написал решение этих двух неравенств на двух листках ===>>
Приложения:
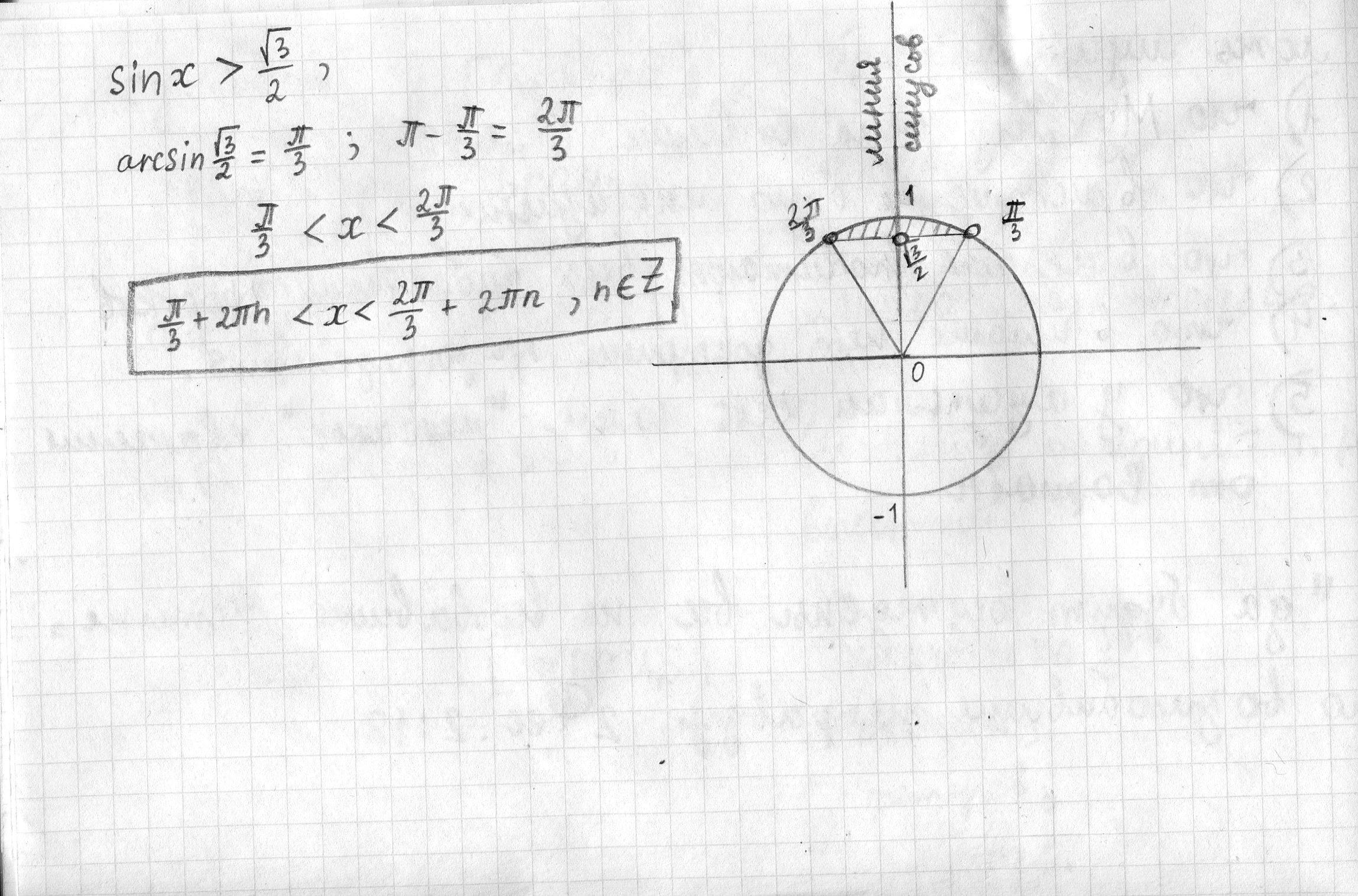
Автор ответа:
1
1)
Приравняем выражение для нахождения корней
, n ∈ Z
Это решение можно записать в совокупность
, n ∈ Z
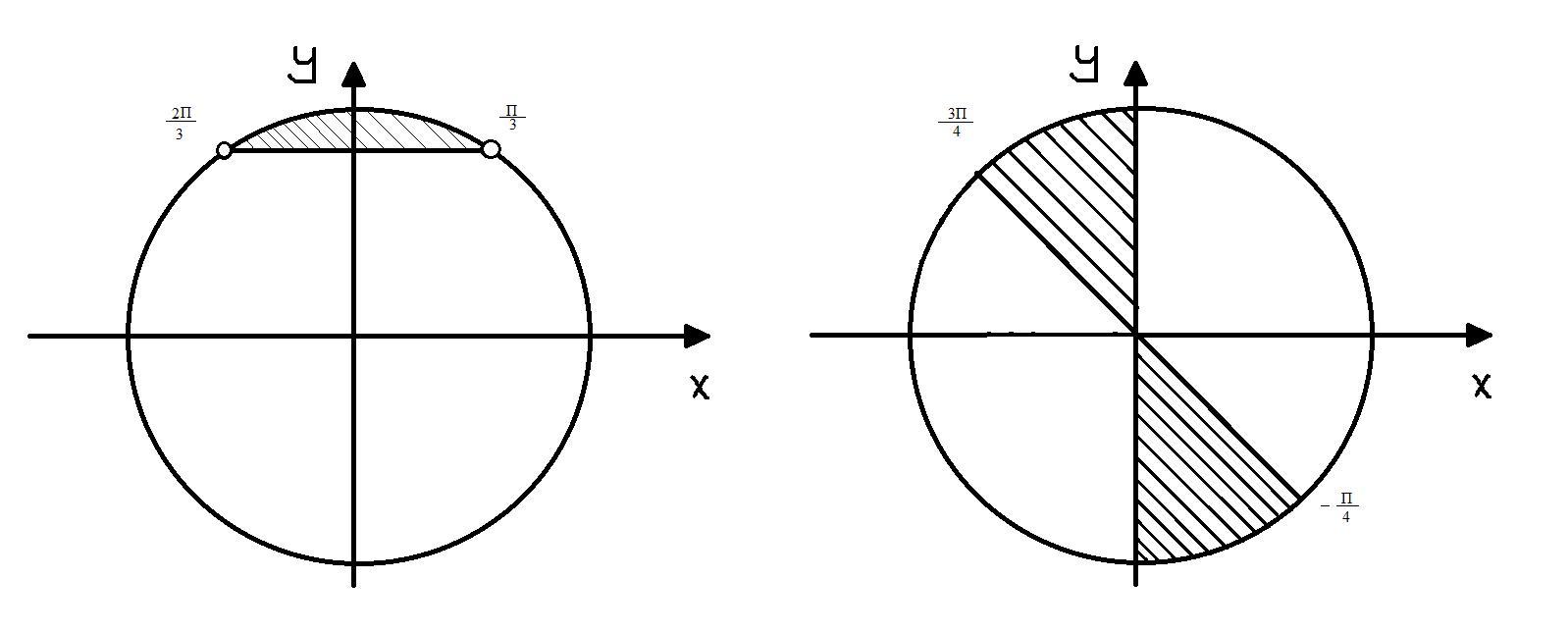
Из рисунка(вложения) видно, что решения, которые больше, находятся выше решений уравнения
Из этого следует, что решением неравенства является
, n ∈ Z
2)
Снова приравняем выражение для нахождения корней
, n ∈ Z
Котангенс и тангенс отрицательны во 2 и 4 четвертях и решение будет как на 2 рисунке во вложении,т.е
x ∈ , n ∈ Z
Приложения:
Похожие вопросы
Предмет: Английский язык,
автор: Аноним
Предмет: Английский язык,
автор: БОЖЕСТВОLove
Предмет: Русский язык,
автор: найтислова
Предмет: Русский язык,
автор: роса10леи
Предмет: Алгебра,
автор: katilvkatil