Question

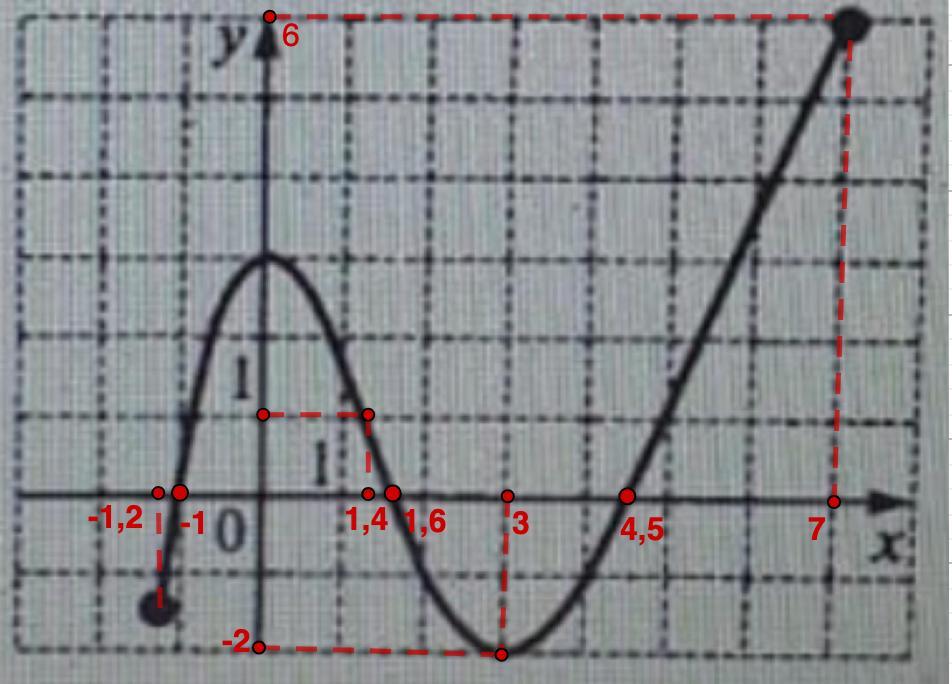
На рисунке изображён график функции y=f(x). Пользуясь графиком найдите:
а) область определения функции
б) область значений функции
в) f(3)
г) значения x, при которых f(x)=1
д) координаты точек пересечения с осью x
е) значение аргумента, при которых значение функции отрицательны
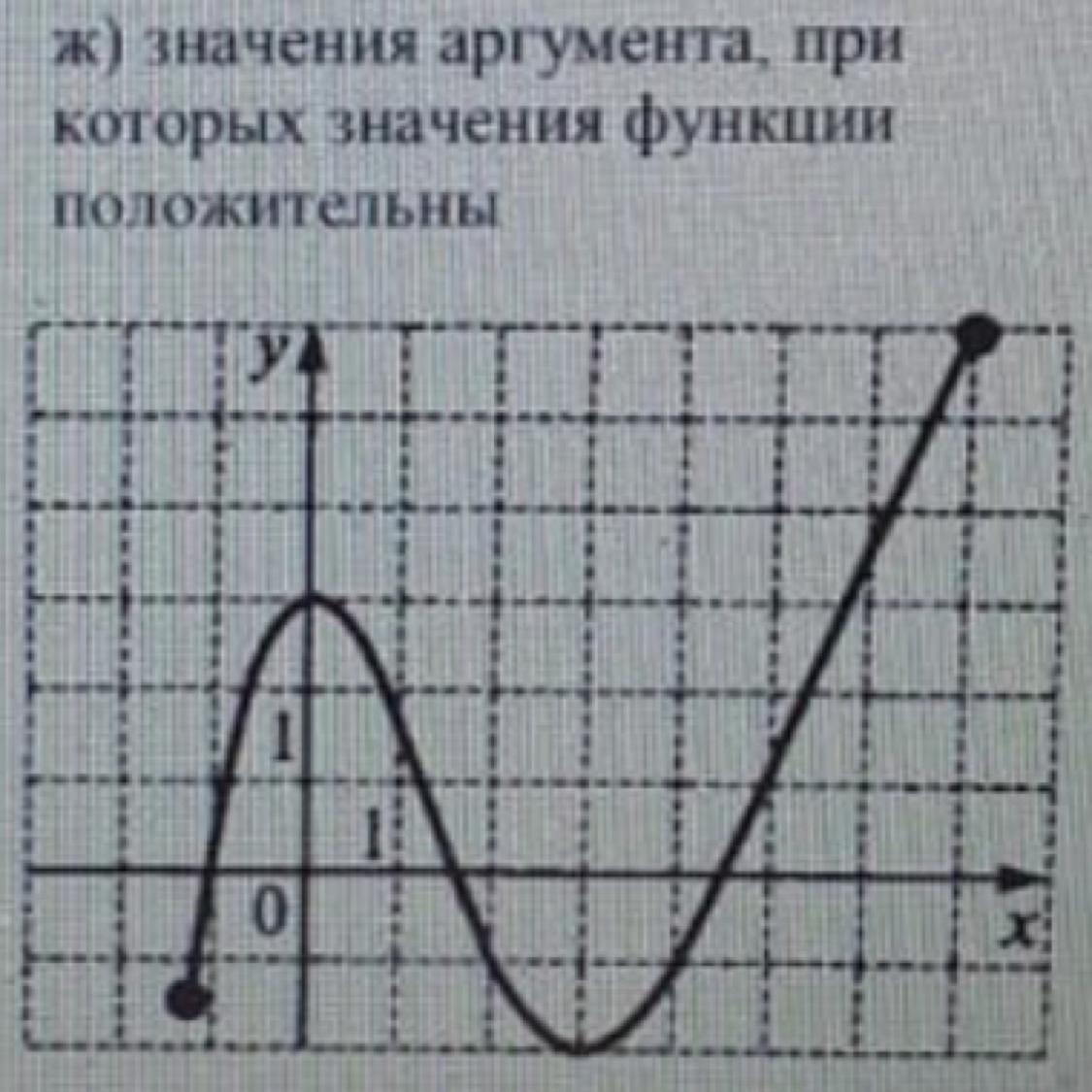
ж) значение аргумента, при котором значение функции положительны.
ПОМОГИТЕ ПОЖАЛУЙСТА ДАМ 45 БАЛЛОВ

Answer 1

Ответ:

а) х ∈ [-1,2; 7]

б) y ∈ [-2; 6]

в) f (3) = -2

г) f (x) = 1; x = 1,4

д) (-1; 0); (1,6; 0); (4,5; 0)

е) х ∈ (-1,2; -1) ∪ (1,6; 4,5)

ж) х ∈ (-1; 1,6) ∪ (4,5; 7)

Объяснение:

На рисунке изображён график функции y=f(x).

Пользуясь графиком найти:

а) область определения функции:

• Область определения — множество значений х.

х ∈ [-1,2; 7]

б) область значений функции.

• Множество значений функции — множество всех значений, которые функция принимает на области определения.

y ∈ [-2; 6]

в) f(3)

Отметим на оси Ох точку с координатой 3, проведем  перпендикуляр к оси Ох до пересечения с графиком, затем из этой точки пересечения опустим перпендикуляр на ось Оу и получим искомую ординату:

f (3) = -2

г) значения x, при которых f(x) = 1.

Здесь отметим на оси Оу ординату 1, проведем  перпендикуляр к оси Оу до пересечения с графиком, затем из этой точки пересечения опустим перпендикуляр на ось Ох и получим искомую абсциссу:

f (x) = 1; x = 1,4

д) координаты точек пересечения с осью x:

В точках пересечения с осью Ох у=0.

(-1; 0); (1,6; 0); (4,5; 0)

е) значение аргумента, при которых значение функции отрицательны.

То есть, найти промежутки, на которых график лежит ниже оси Ох.

х ∈ (-1,2; -1) ∪ (1,6; 4,5)

ж) значение аргумента, при котором значение функции положительны.

То есть, найти промежутки, на которых график лежит выше оси Ох.

х ∈ (-1; 1,6) ∪ (4,5; 7)