Предмет: Алгебра,
автор: Пазенко
Помогите пожалуйста по алгебре
Приложения:
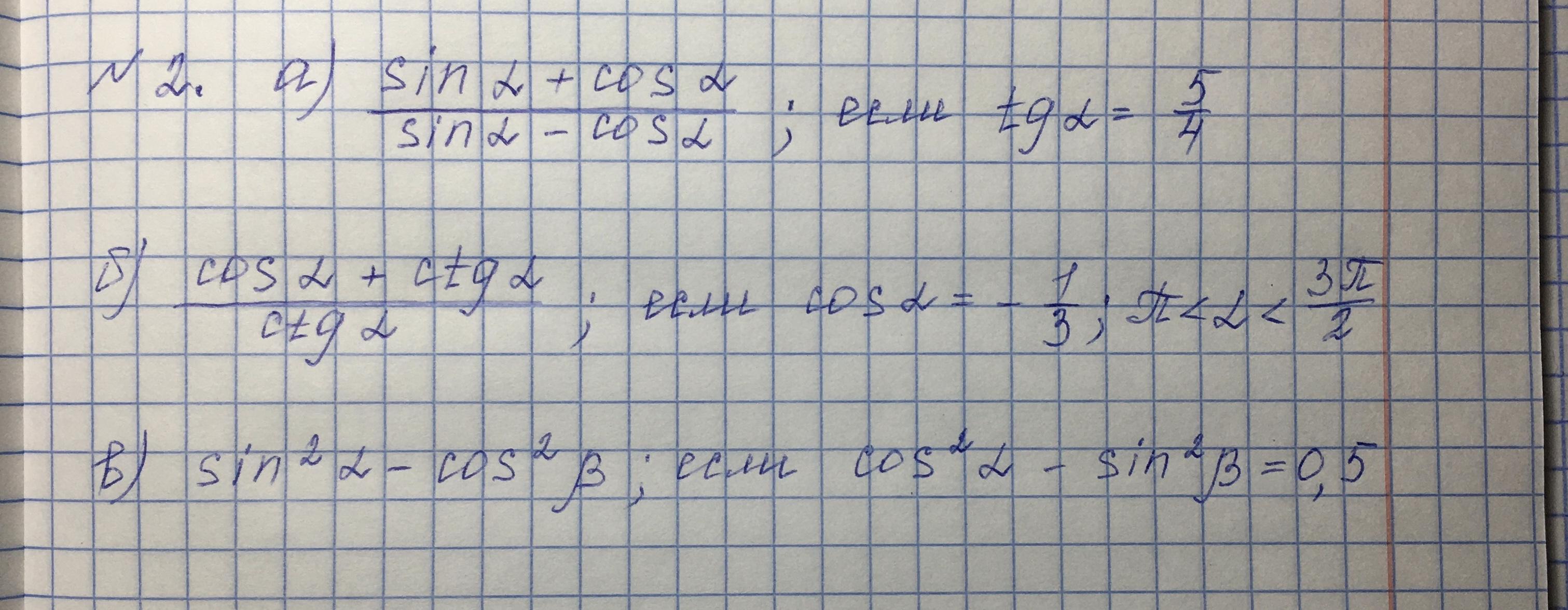
Ответы
Автор ответа:
1
Пазенко:
Спасибо огромное!!!
Похожие вопросы
Предмет: Другие предметы,
автор: ника1251
Предмет: Английский язык,
автор: Аноним
Предмет: Другие предметы,
автор: мия2
Предмет: Обществознание,
автор: enoqarushanyan