Предмет: Алгебра,
автор: ajnara
40 баллов.Найдите производные заданной функции
Приложения:
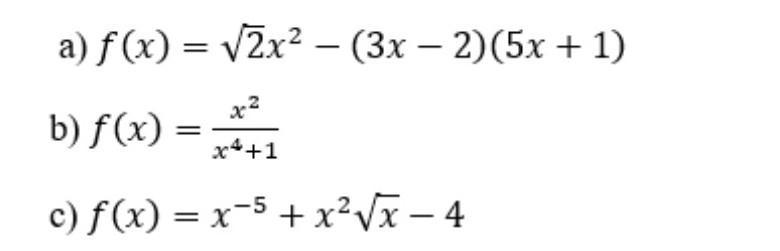
Ответы
Автор ответа:
0
Ответ:
а
б
с
Похожие вопросы
Предмет: Русский язык,
автор: taiskim1
Предмет: Русский язык,
автор: deniskaegorov
Предмет: Английский язык,
автор: Kiesza
Предмет: Биология,
автор: LizaDo
Предмет: Русский язык,
автор: pivovarovakatau