Question

Расскажите как это делается. На снимках представлены задания из учебника и их решения. Непонятно как это вычислить используя геометрические соображения.

Answer 1

Подинтегральная функция описывает окружность.
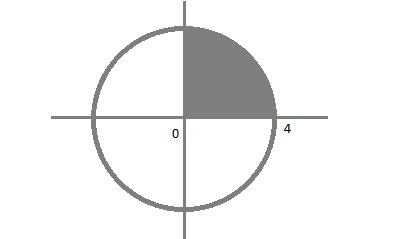
В первом примере это y²+x²=16 - окружность с центром в начале координат и радиусом 4. Следовательно итеграл с границами от 0 до 4 - площадь четвертой части круга с радиусом 4, что равно 1/4 π*R²=1/4 π*16.

Во вторм случае аналогично окружность с радиусом 5 и центром в начале координат.

Answer 2

в примере a) надо найти площадь отсеченную некой кривой, прямой х, прямой х=0 и прямой х=4
нетрудно заметить, что у=корень(16-x^2) - часть окружности x^2+y^2=4^2
таким образом искомый интеграл равен четвертой части площади круга с радиусом 4
а именно 1/4* pi * 4^2 = 4*pi

аналогично, в примере б) надо найти площадь отсеченную некой кривой, прямой х, прямой х=-5 и прямой х=0
нетрудно заметить, что у=корень(25-x^2) - часть окружности x^2+y^2=5^2
таким образом искомый интеграл равен четвертой части площади круга с радиусом 5
а именно 1/4* pi * 5^2 = pi*25/4