Предмет: Математика,
автор: markusyrs
Помогите пожалуйста !! Диф-ур
Приложения:
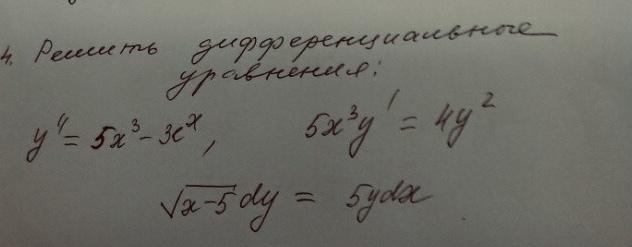
Ответы
Автор ответа:
2
markusyrs:
Спасибо большое, лучший!
Похожие вопросы
Предмет: Русский язык,
автор: Аноним
Предмет: Русский язык,
автор: Elenna1
Предмет: Русский язык,
автор: yfui
Предмет: Математика,
автор: natudenisa