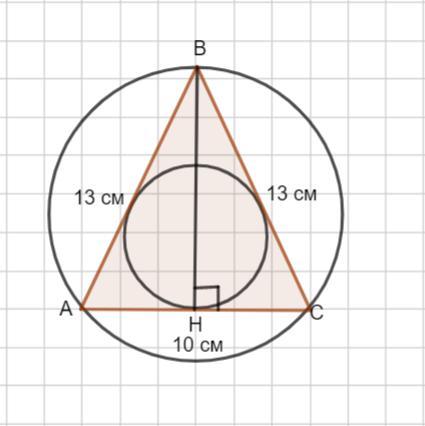
в равнобедренном треугольнике боковая сторона равна 13 см,
основание равно 10 см. Найдите радиус вписанной в этот треугольник и радиус
описанной около этого треугольника окружности.
Ответы
Ответ:
Радиус окружности вписанной в треугольник см, а радиус окружности, описанной около треугольника
см
Объяснение:
Пусть дан ΔАВС - равнобедренный.
АВ=ВС= 13 см, АС =10 см .
Проведем высоту ВН к основанию, в равнобедренном треугольнике высота, проведенная к основанию является медианой. Тогда АН=НС= 10:2=5 см.
Рассмотрим Δ АНВ - прямоугольный. Применим теорему Пифагора : в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
Значит, высота BH =12 см.
Найдем площадь ΔАВС
S= 60 см².
Радиус окружности, вписанной в треугольник найдем по формуле :
где S- площадь треугольника , P- периметр треугольника.
Тогда радиус окружности. вписанной в треугольник см.
Радиус окружности, описанной около треугольника найдем по формуле :
Значит, а радиус окружности, описанной около треугольника будет см