Question

ТЕКСТ ЗАДАНИЯ
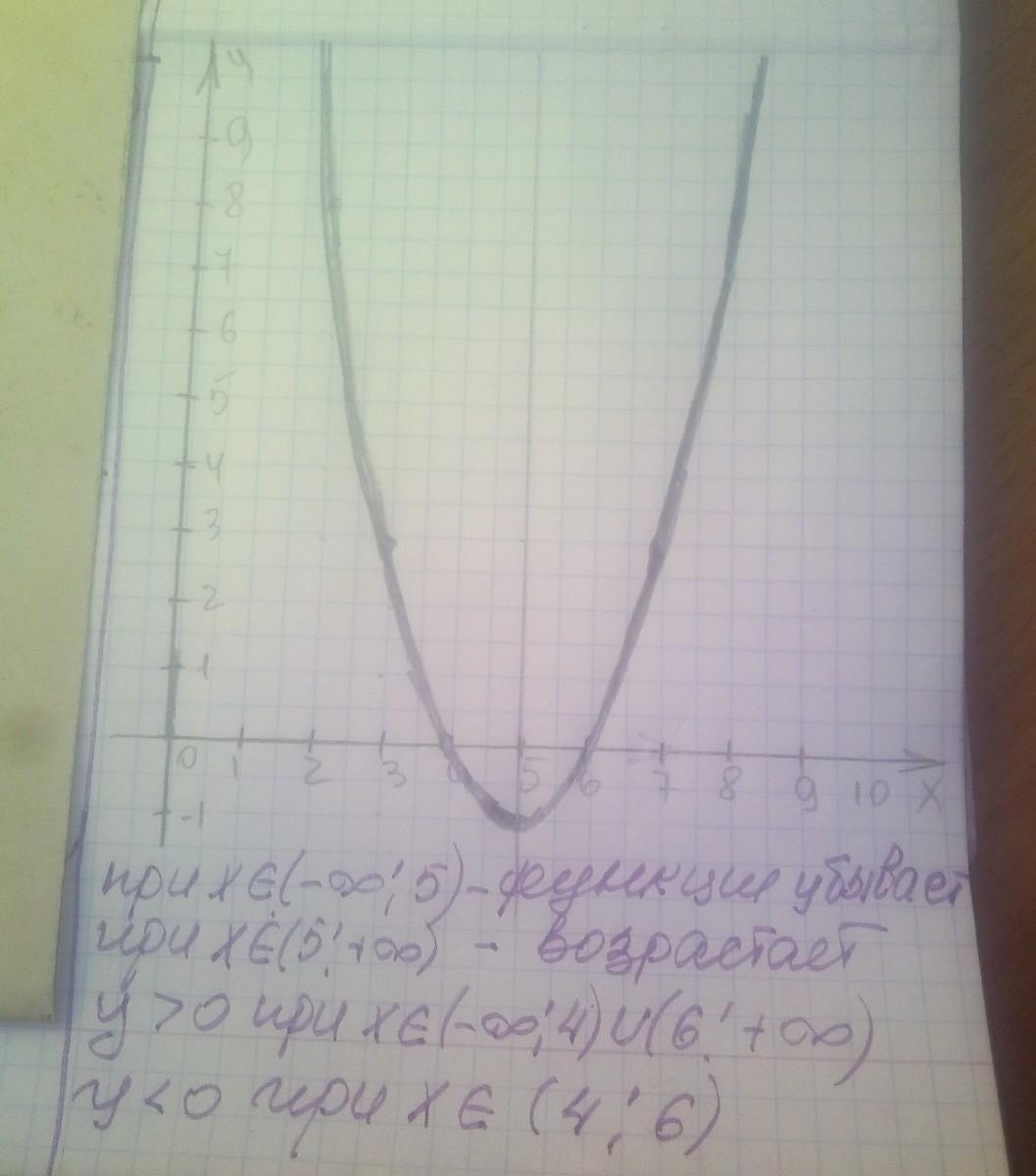
Опиши свойства квадратичной функции y=x2-10x +24

ДИМА РЕШИ 40 БАЛЛОВ КАК И ОБЕЩАЛ
а) D(y) =
б) E(y)=
в) Вершина параболлы – (0)
г) функция возрастает на промежутке xe 0
д) функция убывает на хє (0)
е) нули функции x1=; х2=
ж) построй график заданной функции.

Answer 1

Ответ:

решение смотри на фотографии

Answer 2

а) $D(y): x\in R \ \ \ \ \ \ (-\infty;+\infty)$

б)

$y'=(x^2-10x+24)'=2x-10=2\cdot (x-5)\\ 2\cdot(x-5)=0; \\ x-5=0; \\ x=5; \\ y(5)=5^2-10\cdot 5+25=25-50+24=-1; \\ \\ E(y): y\in R; \ \ y\geq -1 \ \ \ \ [-1;+\infty)$

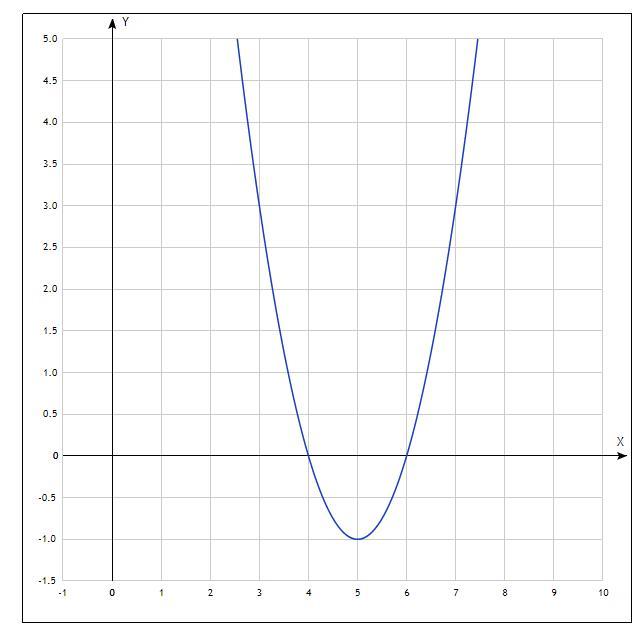
в) вершина параболы:

$x=-\frac{b}{2a}=-\frac{(-10)}{2\cdot 1}=\frac{10}{2}=5; \\ \\ y=5^2-10\cdot 5 +24=-1; \\ \\ (5;-1)$

г) возрастает на промежутке $x\in (5;+\infty)$

д) т.к. a>0, то функция убывает на промежутке $x\in(-\infty;5)$

е)

$x^2-10x+24=0; \\ \\ x_{1,2}=\frac{-(-10)\pm\sqrt{(-10)^2-4\cdot1\cdot 24}}{2\cdot 1}=\frac{10\pm\sqrt{100-96}}{2}=\frac{10\pm2}{2}; \\ \\ x_1=\frac{10+2}{2}=\frac{12}{2}=6; \ \ \ \ \ \ x_2=\frac{10-2}{2}=\frac{8}{2}=4$

ж) на фото