Question

ОЧЕНЬ СРОЧНО РЕБЯТ !!!!!

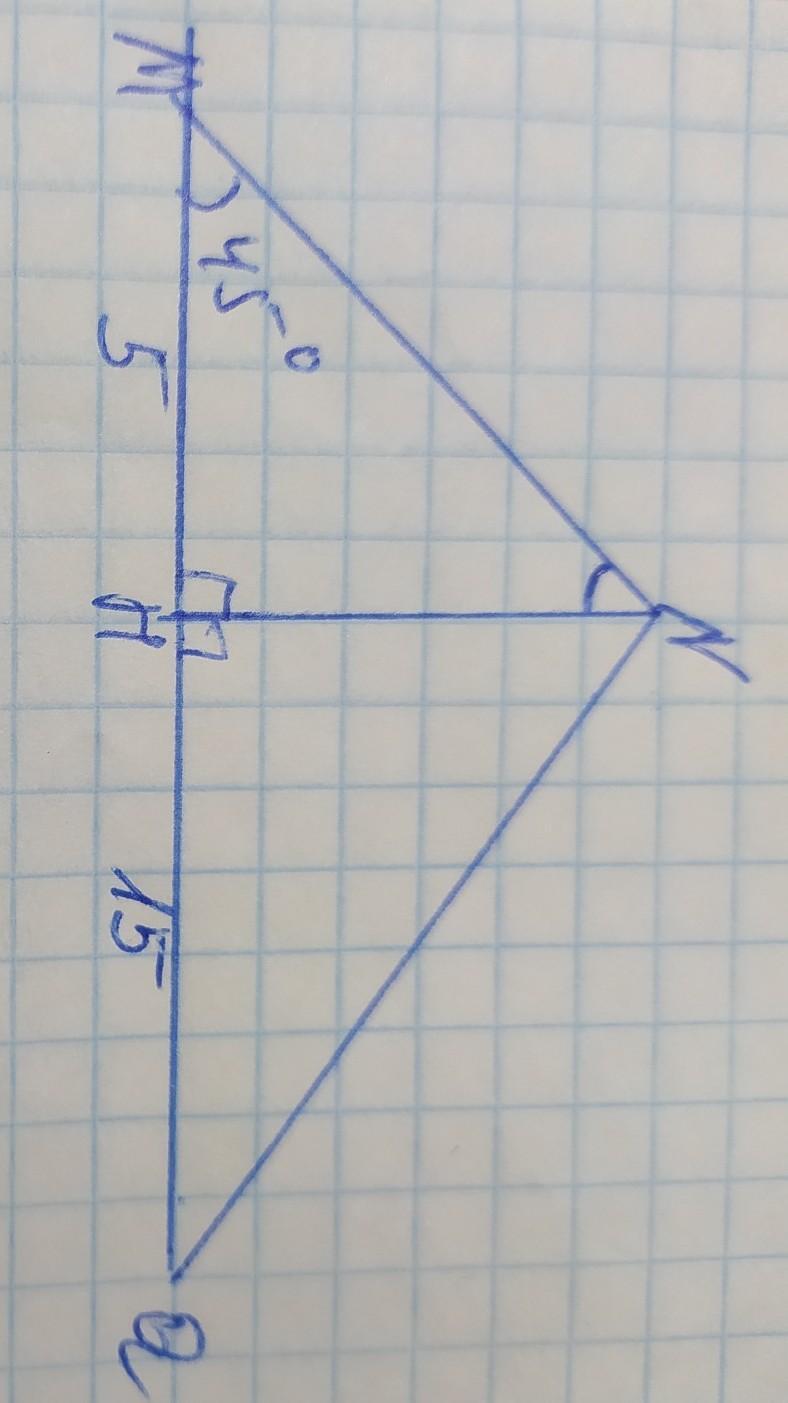
треугольнике MNQ2M = 45 °, а высота NH делит сторону на отрезки МН и Н соответственны равные 5 см и 15 см. Найдите площадь треугольника MNQ.​

Answer 1

Ответ:

S∆MNQ=50см²

Объяснение:

Если я правильно поняла, что угол М=45°, МН=5см, HQ=15см, то в этом случае решение следующее:

высота NH делит ∆MNQ на 2 прямоугольных треугольника : MNH и NQH. Рассмотрим ∆MNH.

Угол М=45°, а сумма острых углов прямоугольного треугольника равна 90°, поэтому угол MNH=90–45=45°. Угол М= углуMNH=45°, значит ∆MNH - равнобедренный, поэтому МН=NH=5см.

MQ =MH+HQ=5+15=20см

Площадь треугольника вычисляется по формуле:

$\\ s = \frac{1}{2} \times mq \times nh = \frac{1}{2} \times 20 \times 5 = \\ = \frac{100}{2} = 50$