Предмет: Математика,
автор: Olegnus
ДАЮ 60 БАЛЛОВ
Помогите пожалуйста, решить 2 интеграла на фото.
2 задание найти при помощи интеграла площадь фигуры ограниченной точками
Y=Х^3
Y=0
X=2
Приложения:
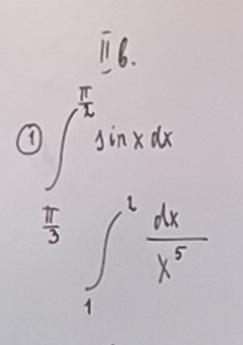
Ответы
Автор ответа:
0
Ответ:
Пошаговое объяснение:
1
2
3
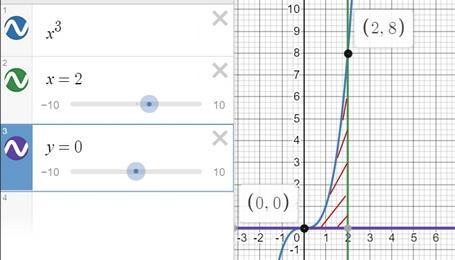
y=x³ y=0 x=2
все данные берем из графика
Приложения:
Похожие вопросы
Предмет: Қазақ тiлi,
автор: дюхаамахасла
Предмет: Русский язык,
автор: 9190222657
Предмет: Русский язык,
автор: катькафа
Предмет: Английский язык,
автор: MarkuzZema