Предмет: Математика,
автор: DiscoPartizan
Помогите найти производную неявной функции.
Приложения:
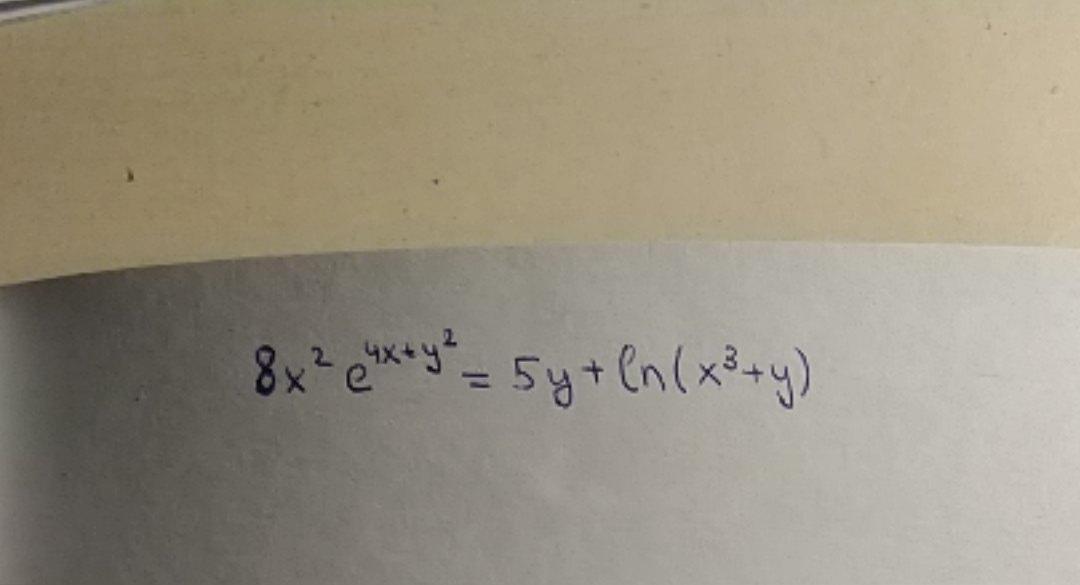
Ответы
Автор ответа:
1
Ответ:
Похожие вопросы
Предмет: Русский язык,
автор: matveeva78
Предмет: Русский язык,
автор: Аноним
Предмет: Немецкий язык,
автор: Ульчик43
Предмет: Математика,
автор: VaReNiK37
Предмет: Математика,
автор: 7nikiforov