Предмет: Геометрия,
автор: Аноним
Срочно!!!!!Найдите катеты и высоту прямоугольного треугольника, проведённую из вершины прямого угла, если она делит гипотенузу на отрезки длинной 4 см и 16 см
Ответы
Автор ответа:
1
В прямоугольном треугольнике АВ и АС - катеты, ВС - гипотенуза, АН - высота.
ВН = 4 см; СН = 16 см;
По теореме Пифагора
из тр - ка АВС: ВС² = АВ² + АС²;
из тр - ка АВН: АВ² = ВН² + АН²;
из тр - ка АСН: АС² = АН² + CH²;
Из двух послед. выраж.:
АВ² + BC² = BH² + AH² + AH² + HC²; AB² + BC² = 2 * AH² + BH² + CH²;
2 * AH² = (AB² + BC²) - BH² - CH²;
AB² + BC² = (BH + CH)² = (4 + 16)² = 400 (см²);
BH² = 4² = 16 (cм²); CH² = 16² = 256 (см²);
2 * AH² = 400 - 16 - 256 = 128 (см); AH² = 64 cм²;
АН = √64 = 8 (см).
ВН = 4 см; СН = 16 см;
По теореме Пифагора
из тр - ка АВС: ВС² = АВ² + АС²;
из тр - ка АВН: АВ² = ВН² + АН²;
из тр - ка АСН: АС² = АН² + CH²;
Из двух послед. выраж.:
АВ² + BC² = BH² + AH² + AH² + HC²; AB² + BC² = 2 * AH² + BH² + CH²;
2 * AH² = (AB² + BC²) - BH² - CH²;
AB² + BC² = (BH + CH)² = (4 + 16)² = 400 (см²);
BH² = 4² = 16 (cм²); CH² = 16² = 256 (см²);
2 * AH² = 400 - 16 - 256 = 128 (см); AH² = 64 cм²;
АН = √64 = 8 (см).
Автор ответа:
1
Ответ:
8 см 8√5 см 4√5 см
Объяснение:
h=√(4*16)=8 cм
по теореме Пифагора:
b=√(8²+16²)=√(64+256)=√320=8√5 см
a=√(8²+4²)=√(64+16)=√80=4√5 cм
Приложения:
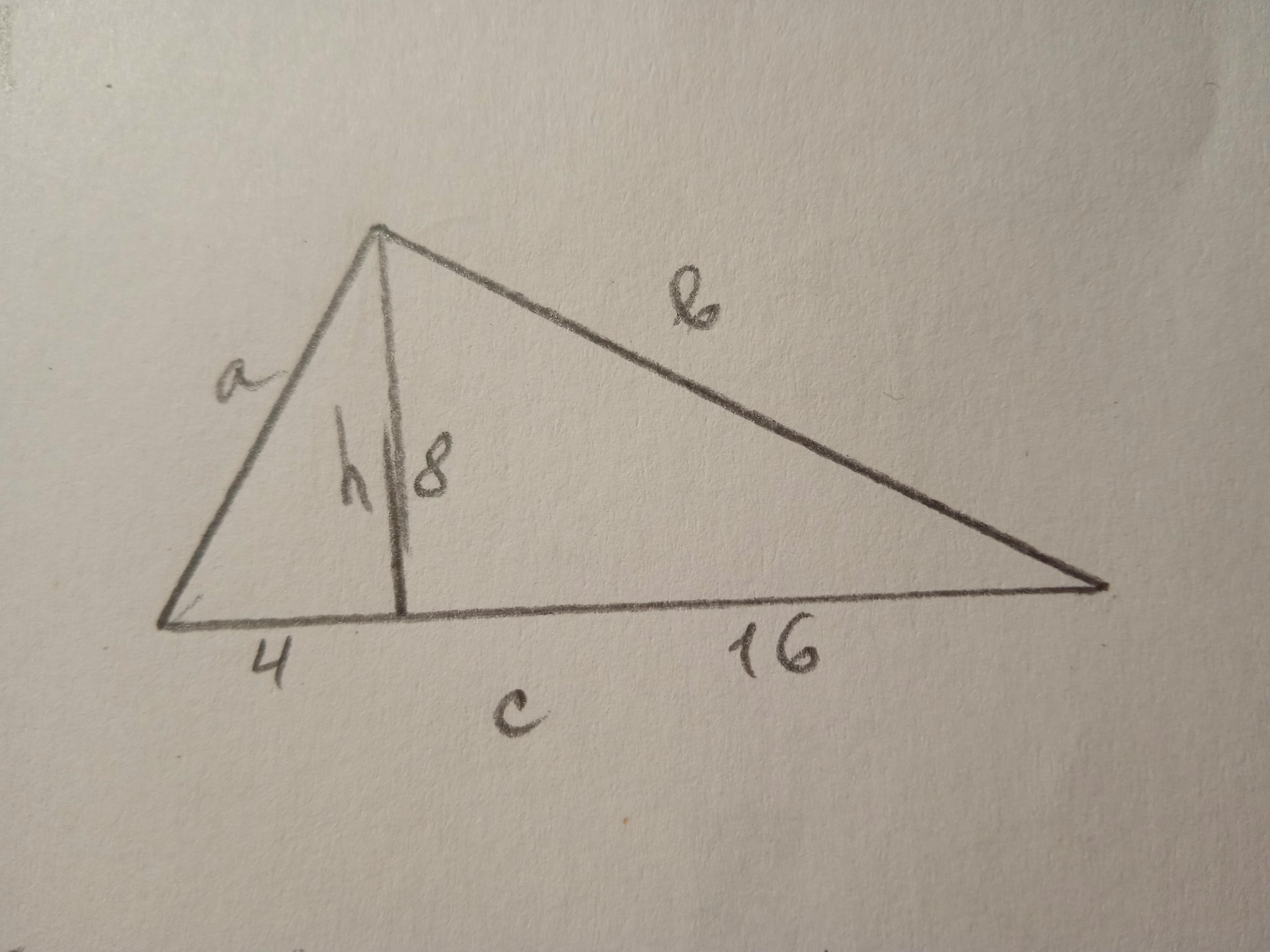
Похожие вопросы
Предмет: Русский язык,
автор: alesa555
Предмет: Окружающий мир,
автор: Kasatkevicha
Предмет: Русский язык,
автор: litynba
Предмет: Математика,
автор: romankoruslan