Question

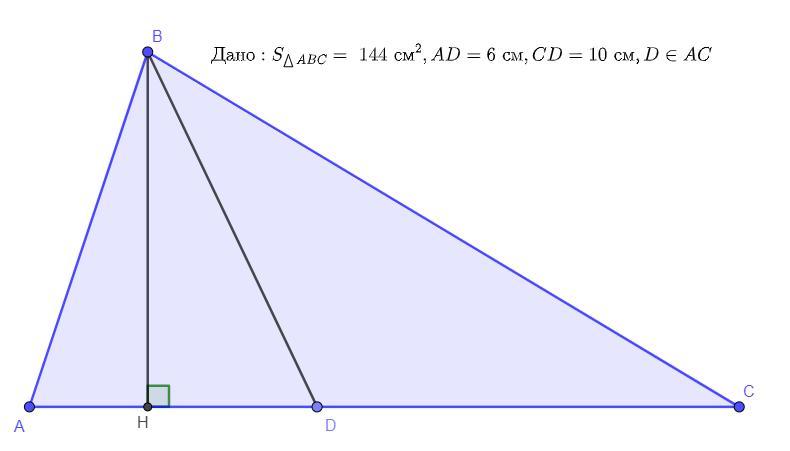
Дан треугольник ABC, на стороне AC которого взята точка D такая, что AD=6 см, а DC=10 см. Отрезок DB делит треугольник ABC на два треугольника. При этом площадь треугольника ABC составляет 144 см2.
Найди площадь большего из образовавшихся треугольников, ответ дай в квадратных сантиметрах.

Answer 1

Ответ:

$\boxed{S_{зBCD} =90}$ см²

Объяснение:

Дано: AD = 6 см, DC = 10 см, D ∈ AC, $S_{зABC} = 144$ см²

Найти: $S_{зBAD}, S_{зBDC}$ - ?

Решение:

Из точки B проведем перпендикуляр на прямую AC в точку H. Отрезок BH - высота в треугольнике ΔABC, ΔBAD, ΔBDC по определению высоты в треугольнике.

По основному свойству отрезка: AC = AD + DC = 10 + 16 = 16 см.

По формуле площади треугольника:

$S_{зABC} = \dfrac{BH \cdot AC}{2} \Longrightarrow BH = \dfrac{2S_{зABC}}{AC} = \dfrac{2 \cdot 144}{16} = \dfrac{288}{16} = 18$ см.

$\boxed{S_{зBCD} = \dfrac{BH \cdot DC}{2} = \dfrac{18 \cdot 10}{2} = \dfrac{180}{2} = 90}$ см².

$S_{зBAD} = \dfrac{BH \cdot AD}{2} = \dfrac{6 \cdot 18}{2} = 6 \cdot 9 = 54$ см².

$S_{зBCD} > S_{зBAD} \Longrightarrow S_{зBCD}$ - имеет наибольшую площадь.