Question

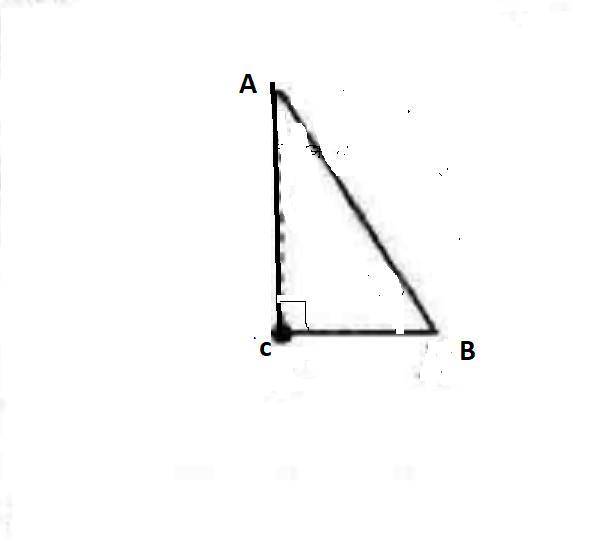
В прямоугольном треугольнике ABC, AB-гипотенуза, угол B равен 60 градусов. Найдите гипотенузу и меньший катет треугольника, если известно, что их сумма равна 29.1 см​

Answer 1

Ответ: АВ=19,4 см, ВС=9,7 см

Решение:

Дано:ΔАВС,∠ С=90°,∠ В=60°, АВ+СВ=29,1 см

Найти: АВ-?, СВ-?

Решение:

По теореме о сумме острых углов прямоугольного треугольника

∠А+∠В=90°

∠А=90°-∠В=90°-60°=30°.

Так как СВ- катет против угла в 30°, то он равен половине гипотенузы.

Пусть СВ=х, тогда АВ= 2СВ=2х

х+2х=29,1;

3х=29,1;

х=29,1:3;

х=9,7(см)

СВ=9,7 см

АВ= 2*9,7 см= 19,4 см