Предмет: Алгебра,
автор: rizeeuijj
алгебра 9 класс помогите дам 40 баллов!!!до завтра
Приложения:
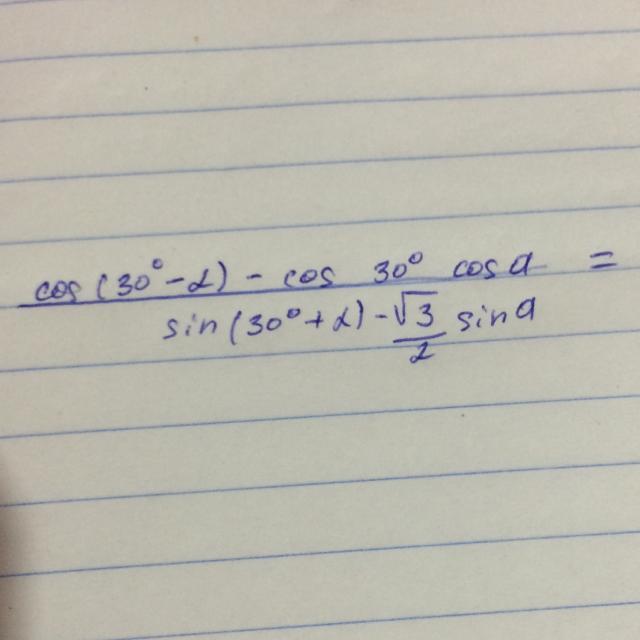
Ответы
Автор ответа:
1
Ответ:
rizeeuijj:
спасибо!!!
Автор ответа:
1
спасибо!!!
Похожие вопросы
Предмет: Окружающий мир,
автор: Аноним
Предмет: Українська мова,
автор: sonyasfhikm
Предмет: Русский язык,
автор: arsienieva1966
Предмет: Русский язык,
автор: РодиоШумайлов
Предмет: Геометрия,
автор: Bisheps