Question

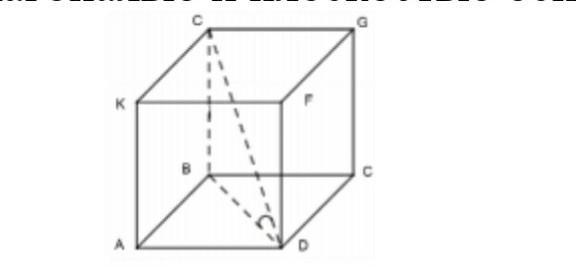
1. В прямоугольном параллелепипеде измерения равны 3, 4, 5. Найдите диагональ параллелепипеда и угол между диагональю и плоскостью основания.

​

Answer 1

Ответ:

Диагональ равна 5√2,

угол между диагональю и основанием равен 45°

Объяснение:

• Квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов его измерений:

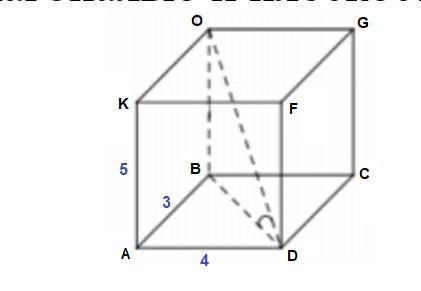
DO² = AB² + AD² + AК²

DO² = 3² + 4² + 5² = 9 + 16 + 25 = 50

DO = √50 = 5√2

BD - проекция диагонали DO на плоскость основания, тогда

∠(OD, (ABC)) = ∠ODB - искомый.

ΔODB:  ∠OBD = 90°,  OB = AК = 5

$\sin\angle ODB=\dfrac{OB}{OD}=\dfrac{5}{5\sqrt{2}}=\dfrac{1}{\sqrt{2}}=\dfrac{\sqrt{2}}{2}$

∠ODB = 45°