Предмет: Геометрия,
автор: ksunya08
Помогите пожалуйста, это очень срочно
найти:
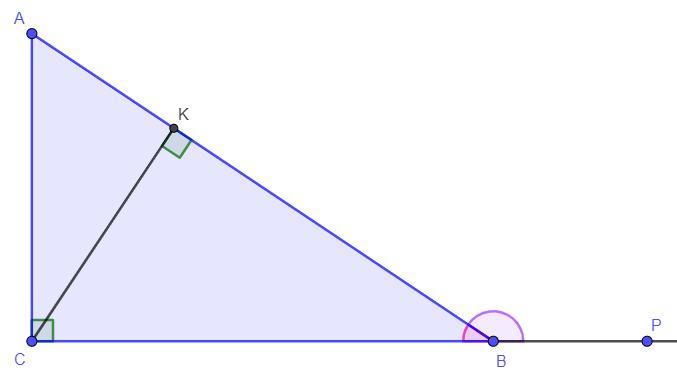
1) острый углы треугольника ABC
2) высоту CK,если BC=14,7 см
Приложения:

Ответы
Автор ответа:
8
Ответ:
∠ABC = 30°
∠CAB = 60°
CK = 7,35 см
Объяснение:
Дано: ∠ACB = 90°, BC = 14,7 см, CK - высота, ∠ABP = 150°
Найти: ∠ABC, ∠CAB, CK - ?
Решение:
Так как угол ∠ABP и ∠ABC - смежные углы, то по свойству смежных углов их сумма 180°, тогда ∠ABP + ∠ABC = 180° ⇒ ∠ABC =
= 180° - ∠ABP = 180° - 150° = 30°.
По теореме про сумму углов треугольника для треугольника ΔABC:
∠ACB + ∠ABC + ∠CAB = 180° ⇒ ∠CAB = 180° - ∠ACB - ∠ABC =
= 180° - 90° - 30° = 90° - 30° = 60°.
По определению косинуса в прямоугольном треугольнике (ΔABC):
см.
см.
По формуле площади прямоугольного треугольника:
см².
По формуле площади треугольника:
см.
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: narminhacimuradova
Предмет: Қазақ тiлi,
автор: Гульнура111
Предмет: Русский язык,
автор: Аноним
Предмет: История,
автор: unicorn242
Предмет: Русский язык,
автор: Lusia544