Question

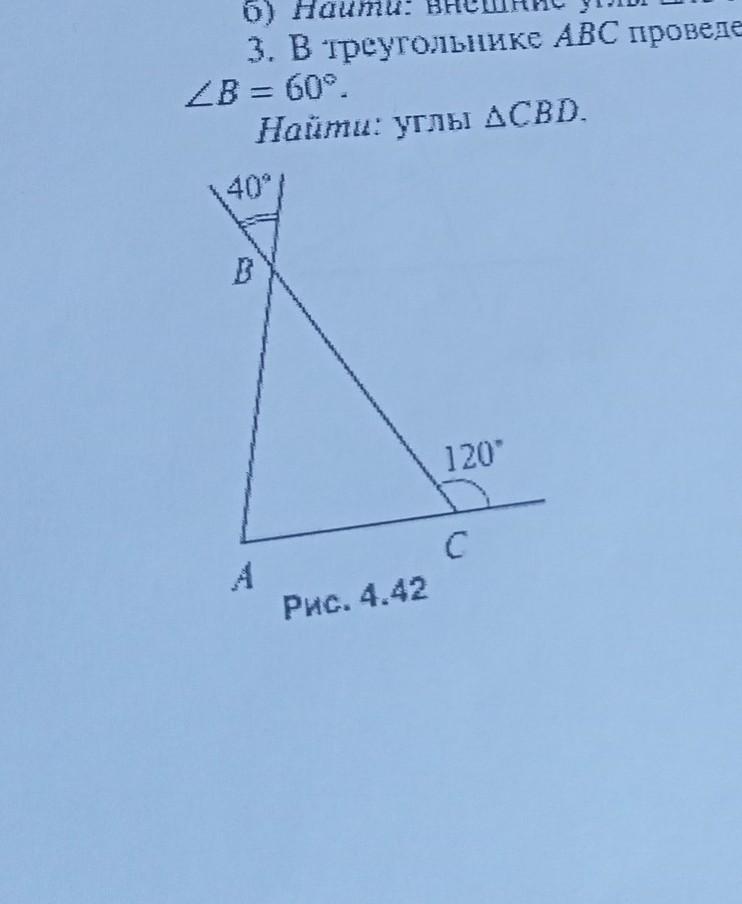
1. Найти: углы АВС (рис. 4,42).
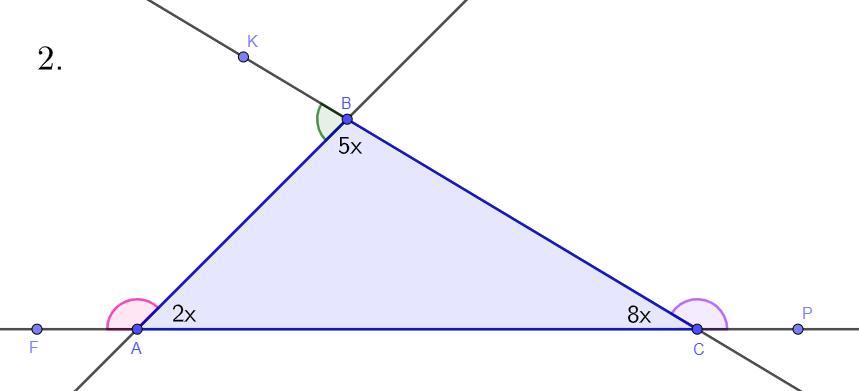
2. Внутренние углы треугольника ABC пропорциональны
числам 2, 5, 8.
а) Найти: углы Авс.
б) Найти: внешние углы ABC.
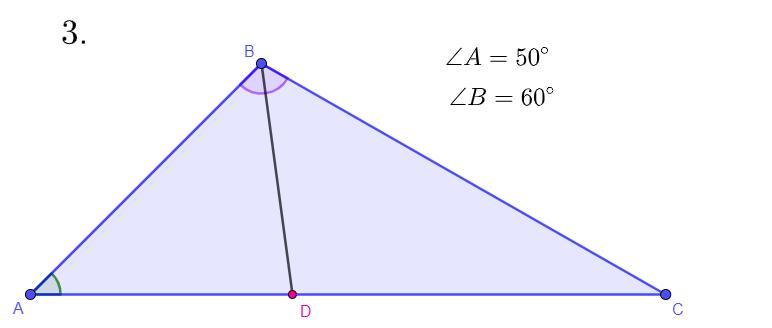
3. В треугольнике ABC проведена биссектриса BD. угол A = 50°.
угол B = 60°.
Найти: углы СВD.
​

Answer 1

Ответ:

1.

∠ABC = 40°

∠BCA = 60°

∠BAC = 80°

2.

∠BAC = 24°

∠ABC = 60°

∠BCA = 96°

∠FAB = 156°

∠KBA = 120°

∠BCP = 84°

3.

∠BCD = 70°

∠CBD = 30°

∠BDC = 80°

Объяснение:

1. Согласно рисунку (4.42)

Угол ∠ABC = 40°, как вертикальные углы

(угол ∠ABC и 40° - вертикальные).

Угол 120° смежный с углом ∠BCA, тогда по свойству смежных углов:

120° + ∠BCA = 180°

∠BCA = 180° - 120° = 60°

По теореме про сумму углов треугольника:

∠ABC + ∠BCA + ∠BAC = 180° ⇒ ∠BAC = 180° - ∠ABC - ∠BCA =

180° - 40° - 60° = 80°.

2.

Дано: ∠BAC : ∠ABC : ∠BCA = 2 : 5 : 8

Найти: ∠BAC, ∠ABC, ∠BCA, ∠FAB, ∠KBA, ∠BCP - ?

Решение:

Введем коэффициент пропорциональности x, тогда по условию задачи ∠BAC = 2x, ∠ABC = 5x, ∠BCA = 8x.

По теореме про сумму углов треугольника (ΔABC):

∠BAC + ∠ABC + ∠BCA = 180°

2x + 5x + 8x = 180°

15x = 180°|:15

x = 12°

∠BAC = 2x = 2 * 12° = 24°.

∠ABC = 5x = 5 * 12° = 60°.

∠BCA = 8x = 8 * 12° = 96°.

По теореме внешний угол треугольника равен сумме двух углов не смежных с ним:

∠FAB = ∠BCA + ∠ABC = 96° + 60° = 156°.

∠KBA = ∠BAC + ∠BCA = 24° + 96° = 120°.

∠BCP = ∠ABC + ∠BAC = 60° + 24° = 84°.

3.

Дано: ∠A = 50°, ∠B = 60°, BD - биссектриса

Найти: ∠CBD, ∠BCD, ∠BDC - ?

Решение:

По теореме про сумму углов треугольника (треугольник ΔABC):

∠A + ∠B + ∠C = 180° ⇒ ∠C = 180° - ∠A - ∠B = 180° - 50° - 60° = 70°.

Угол ∠BCD = ∠C = 70°.

По определению биссектриса делит угол пополам, тогда

∠ABD = ∠CBD = ∠ABC : 2 = ∠B : 2 = 60° : 2 = 30°.

По теореме про сумму углов треугольника (треугольник ΔBCD):

∠BCD + ∠DBC + ∠BDC = 180° ⇒ ∠BDC = 180° - ∠BCD - ∠DBC =

= 180° - 70° - 30° = 80°.