Предмет: Алгебра,
автор: gfgggggg18
Помогите прошу,по возможности расписать
Приложения:
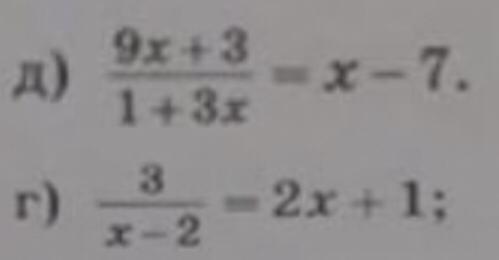
Ответы
Автор ответа:
0
Ответ:
x=10
x1=-1
x2=2,5
Долго росписывать
Автор ответа:
1
Ответ:
Объяснение:
д) ОДЗ:
Решение:
Корень x₂ не удовлетворяет ОДЗ.
___________________________________
г) ОДЗ:
Решение:
Оба корня удовлетворяют ОДЗ.
Похожие вопросы
Предмет: Русский язык,
автор: KoTzAdRoT2014
Предмет: Английский язык,
автор: ангелинасвета
Предмет: Английский язык,
автор: анютка92
Предмет: Математика,
автор: ontop124
Предмет: Математика,
автор: примерка1