Предмет: Алгебра,
автор: hrapdv358
Продиференціювати функцію:
Приложения:

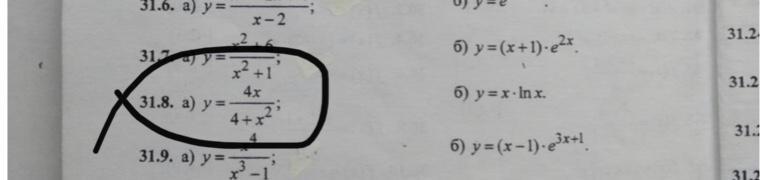
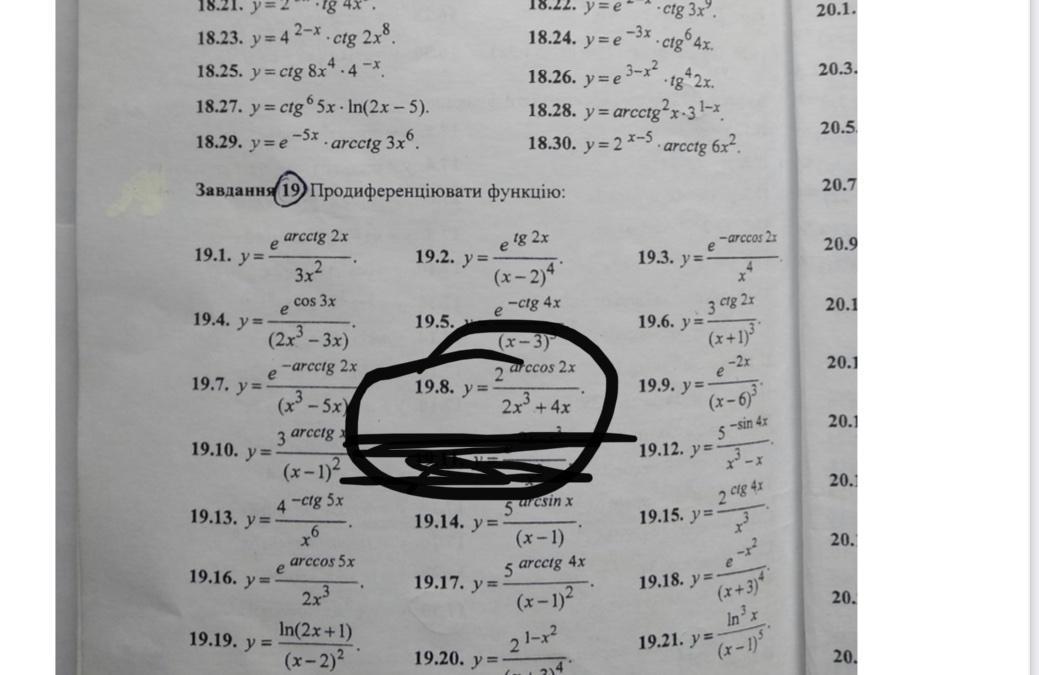
Miroslava227:
на первой фотографии 17.6 или 17.8?
17.8
Ответы
Автор ответа:
2
Ответ:
17.8
31.8
19.8
Похожие вопросы
Предмет: Математика,
автор: Iskhak567
Предмет: Английский язык,
автор: alexmal99
Предмет: Математика,
автор: gula4
Предмет: Химия,
автор: tupikindonbass