Question

ДАЮ 70 БАЛЛОВ СРОЧНО

Знайти периметр п-кутника, якщо у нього всі сторони до­рівнюють по 2 см та: а) п = 7; б) п = 10; в) п = 9.

Скільки діагоналей має опуклий десятикутник?

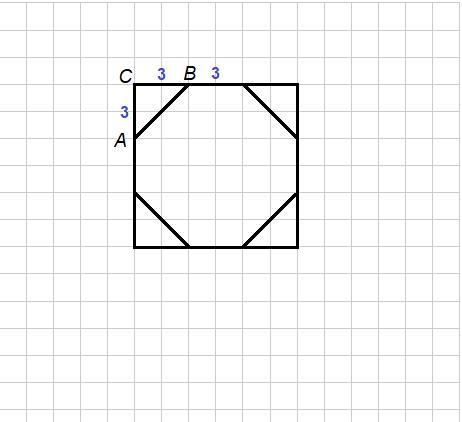
Сторони квадрата поділили на три рівні частини і всі точки поділу послідовно сполучили відрізками. Знайдіть периметр утвореного многокутника, якщо довжина сторони квадрата 9 см. Скільки діагоналей має утворений многокутник?

Опуклий многокутник має 35 діагоналей. Скільки в нього кутів?

Answer 1

Ответ:

1. а) 14 см

  б) 20 см

  в) 18 см

2. 35 диагоналей.

3. Р = 12(1 + √2) см

   20 диагоналей.

4. 10 углов.

Объяснение:

1.

• Периметр многоугольника равен сумме длин всех его сторон.

Если все стороны многоугольника равны а и количество сторон равно n, то его периметр:

P = a · n

a = 2 см

а) n = 7

P = a · n = 2 · 7 = 14 см

б) n = 10

P = a · n = 2 · 10 = 20 см

в) n = 9

P = a · n = 2 · 9 = 18 см

2. Количество диагоналей m выпуклого n-угольника находится по формуле:

$m=\dfrac{n\cdot (n-3)}{2}$

Как получена формула:

• Каждая вершина может быть соединена с (n - 3) вершинами (отнимаем саму вершину и две соседние, всего - 3). Количество диагоналей, проведенных из одной вершины, умножаем на n. Но тогда каждая диагональ будет посчитана дважды, поэтому делим на два.

n = 10

$m=\dfrac{10\cdot (10-3)}{2}=5\cdot 7=35$

Выпуклый десятиугольник имеет 35 диагоналей.

3. Сторона квадрата равна 9 см, значит каждая из трех частей равна 3 см.

Получился восьмиугольник, у которого 4 стороны равны по 3 см (центральный отрезок стороны квадрата) и 4 стороны равны длине отрезка АВ.

Из прямоугольного треугольника АВС по теореме Пифагора:

АВ = √(АС² + ВС²) = √(3² + 3²) = √(3² · 2) = 3√2 см

Периметр многоугольника:

Р = 3 · 4 + 3√2 · 4 = 12 + 12√2 = 12(1 + √2) см

Количество диагоналей найдем по формуле из задачи 2:

$m=\dfrac{n\cdot (n-3)}{2}=\dfrac{8\cdot (8-3)}{2}=4\cdot 5=20$

Всего 20 диагоналей.

4. Количество диагоналей m = 35.

Подставим в формулу из задачи 2:

$m=\dfrac{n\cdot (n-3)}{2}$

$35=\dfrac{n\cdot (n-3)}{2}$         | · 2

70 = n (n - 3)

n² - 3n - 70 = 0

По теореме, обратной теореме Виета:

n₁ = 10

n₂ = - 7 - не подходит по смыслу задачи.

У выпуклого многоугольника 10 углов.