Предмет: Алгебра,
автор: almazovmaks39
найдите производные
Знайдіть похідну
Приложения:
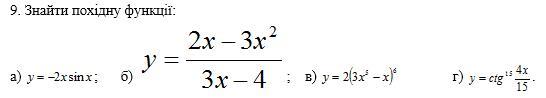
almazovmaks39:
нужен вариант Г
Ответы
Автор ответа:
1
Ответ:
а
б
в
г
Похожие вопросы
Предмет: Литература,
автор: rustamovasakhi
Предмет: Русский язык,
автор: D156
Предмет: Алгебра,
автор: dblackblackbl
Предмет: Английский язык,
автор: сашенька062