Question

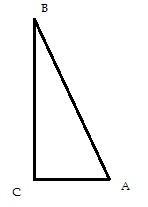
3. [3балла] В прямоугольном треугольнике ABC 2C = 90°, 2А = 60°. Найдите гипотенузу и меньший катет этого
треугольника, если известно, что их сумма равна 34,5 см​. Срочноооооо пожалуйста с чертежом

Answer 1

Ответ:

11,5 см и 23 см

Объяснение:

В Δ АВС катет АС лежит напротив угла В, который равен  90 - 60 = 30°.

Это означает, что катет АС - меньший, а также что он равен половине гипотенузы.

Если обозначить катет АС за Х, то гипотенуза АВ будет 2Х.

Составляем уравнение:

х + 2х = 34,5

3х = 34,5

х = 11,5

Тогла гипотенуза АВ = 23