Предмет: Алгебра,
автор: margrete1810
Помогите, пожалуйста, заранее спасибо
Приложения:
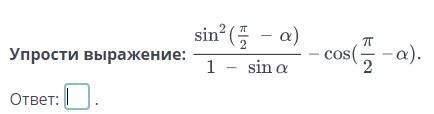
Ответы
Автор ответа:
1
Ответ:
nasty6547:
МОЖЕТ ПОМОЧЬ ПОЖАЛУЙСТА!!!@@
Помоги пожалуйста: https://znanija.com/task/42974670
Автор ответа:
3
Ответ:
Решение:
Ответ: 1.
Похожие вопросы
Предмет: Окружающий мир,
автор: lana2784
Предмет: Английский язык,
автор: albi3
Предмет: Английский язык,
автор: sofica85
Предмет: Химия,
автор: danchikk2000
Предмет: Алгебра,
автор: skiba04