Предмет: Математика,
автор: goodman3372
Найти общее решение дифференциального уравнения 2-го порядка. и Найти частное решение дифференциального уравнения 2-го порядка
Приложения:
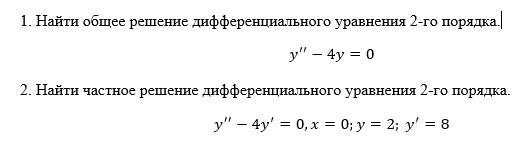
Ответы
Автор ответа:
0
Ответ:
1.
общее решение
2.
общее решение
частное решение
Похожие вопросы
Предмет: Русский язык,
автор: ahmediyaa
Предмет: Беларуская мова,
автор: kilessotatyana
Предмет: Английский язык,
автор: eleneadvadze
Предмет: Литература,
автор: shekero16cfyz
Предмет: Другие предметы,
автор: gggxfhjj