Question

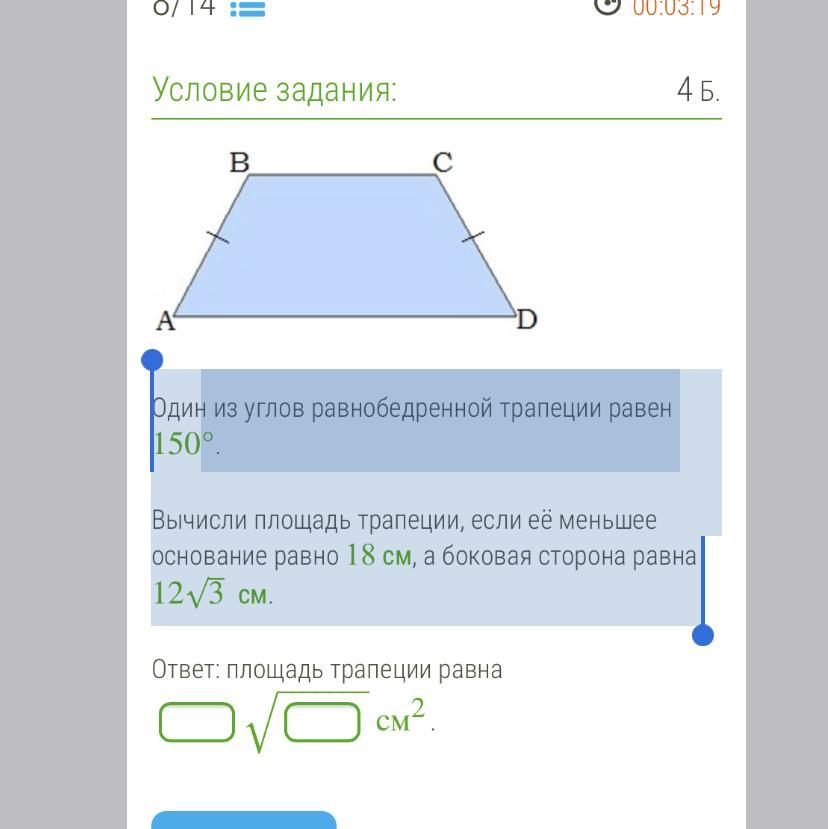
Один из углов равнобедренной трапеции равен 150°.

Вычисли площадь трапеции, если её меньшее основание равно 18 см, а боковая сторона равна 12√ 3см.

Answer 1

Ответ:

506√3 см²

Пошаговое объяснение:

Один из углов равнобедренной трапеции равен 150°. Вычисли площадь трапеции, если её меньшее основание равно 13 см, а боковая сторона равна 22√3 см.

Дано: АВСД - трапеция, АВ=СД=22√3 см.

ВС=13 см.

Найти S.

Решение: Проведем две высоты ВН и СК. Рассмотрим Δ АВН - прямоугольный.

∠АВН=150-90=60°, тогда ∠А=30°, а ВН=12 АВ=11√3 см. (как катет, лежащий против угла 30°)

Найдем АН по теореме Пифагора:

АН²=(22√3)² - (11√3)² = 1452-363=1089; АН=√1089=33 см.

ДК=АН=33 см

АД=АН+КН+ДК=33+13+33=79 см.

S=(13+79):2*11√3=506√3 cм²

Ответ: 506√3 см²