Предмет: Геометрия,
автор: cattt5
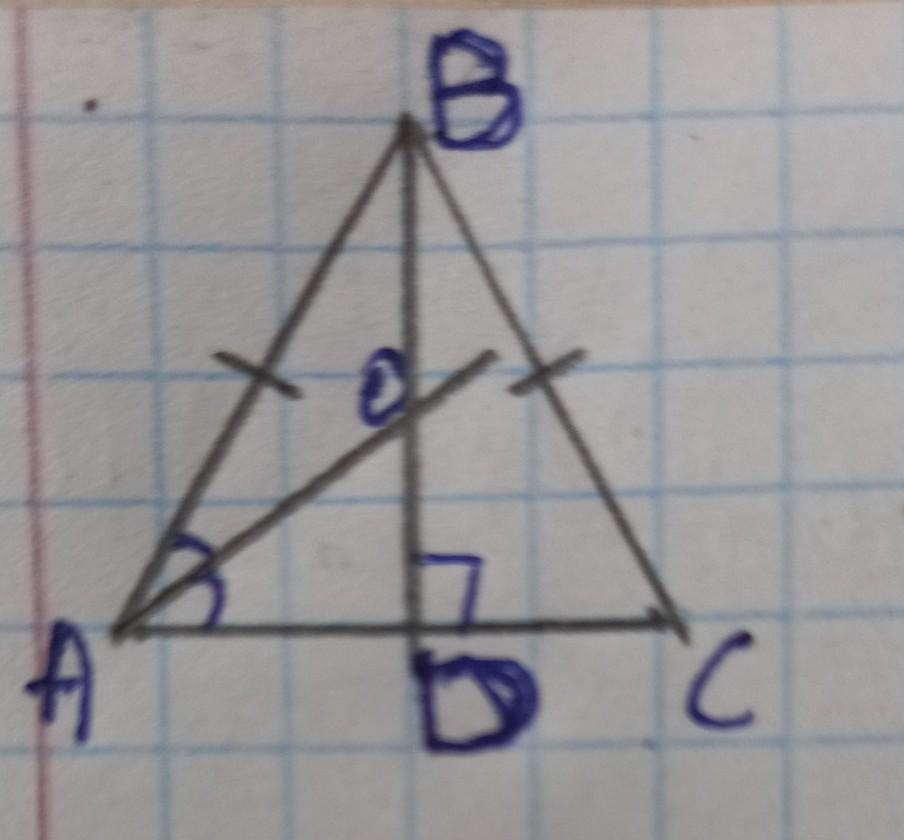
На рисунке АВ=ВС, угол АВС=72 градуса. Отрезок ВD-высота треугольника АВС, луч АО-биссектриса угла ВАС. Найдите градусную меру угла АОD
Приложения:
Ответы
Автор ответа:
1
Ответ:
Объяснение:
равнобедренный ⇒
AO — биссектриса ∠BAC ⇒
Похожие вопросы
Предмет: Русский язык,
автор: Бочковалександр
Предмет: Русский язык,
автор: chepja
Предмет: Русский язык,
автор: vbktyfktdsrbyf
Предмет: Математика,
автор: ольга1710