1. Свободное падение (по вертикали)
Тело бросают вертикально вверх с высоты 15м, оно упало на поверхность
земли через 3 с. Определите скорость бросания тела.
Объясните подробно пожалуйста
Ответы
Дано:
h = 15 м
t = 3 c
g = 10 м/с²
v0 - ?
Решение:
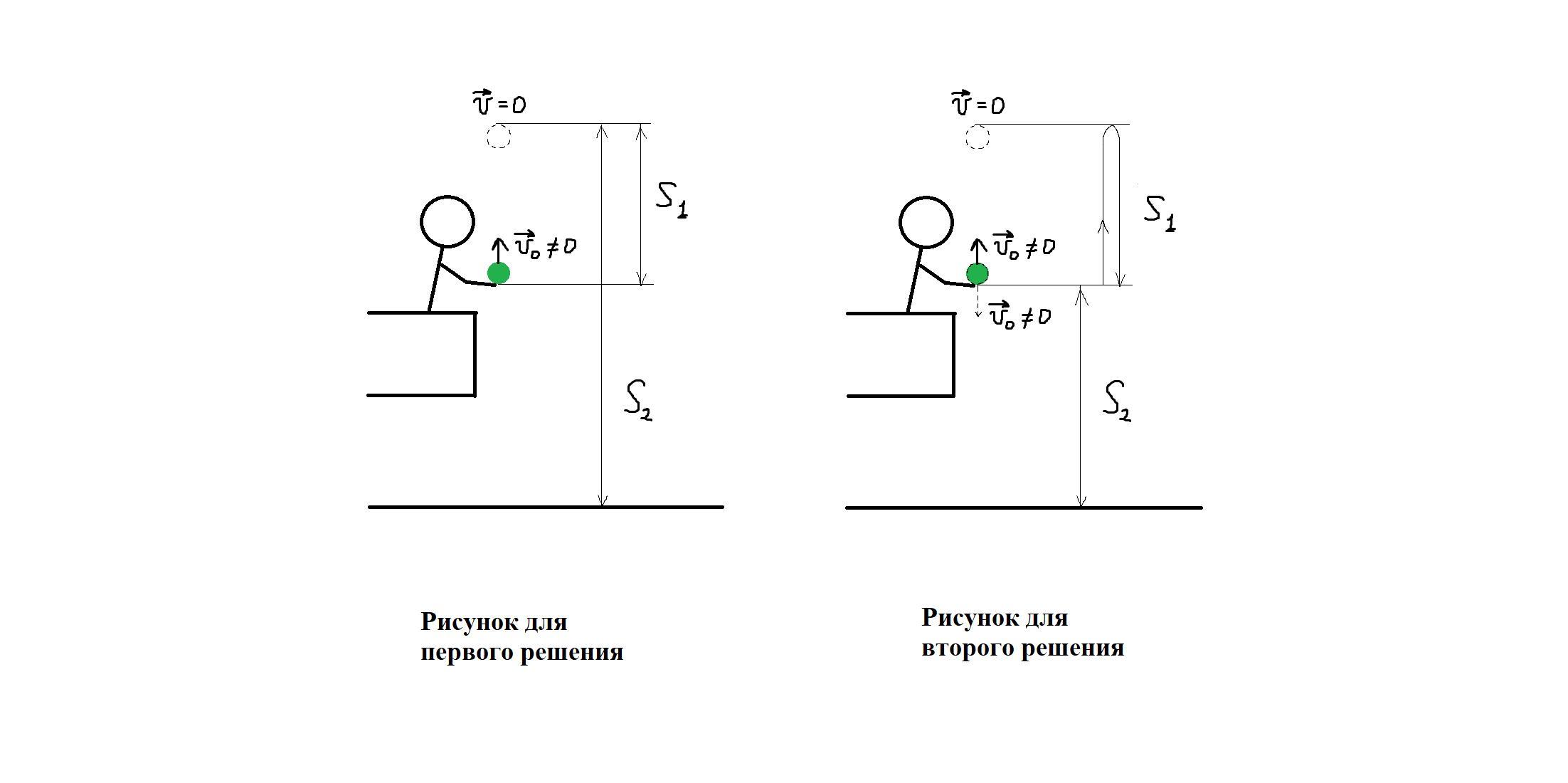
Тело бросают, например, с балкона пятиэтажного дома. Бросают так, что падает тело уже на землю, а не на балкон. Причём движение тела сначала строго вертикально вверх, а потом - строго вертикально вниз. Ну, то есть, если балкон остеклённый, то высунули руку в окно и запустили какой-то предмет строго вертикально вверх. Небольшой резиновый шарик, например. Вот он поднялся до высшей точки, завис на какие-то доли секунды в ней, а потом полетел вниз и столкнулся с асфальтом. И всё это произошло за 3 секунды. Как можно найти начальную скорость шарика? Попробуем разбить общий путь тела на два: путь вверх с начальной скоростью v0 не равной нулю, и путь вниз с начальной скоростью v0 равной нулю (потому что достигнув верхней точки, тело останавливается, а затем свободно падает). Составим уравнение для каждого пути:
S = v0*t - g*t²/2 - путь вверх
S = gt²/2 - путь вниз
Очевидно, что путь вверх занял какое-то определённое время. Как и путь вниз. Значит, время для каждого пути будет различным, тогда уравнения запишем так:
S1 = v0*t1 - g*t1²/2 - путь вверх (знак "минус" перед вторым слагаемым потому, что g направлено вниз, против оси Y, а знак "плюс" перед первым слагаемым потому, что v0 сонаправлена с осью Y).
H' = H - gt'²/2 - путь вниз. Здесь H' - это какая-то высота, которую нужно найти через какое-то время полёта t'. А H - это высота, с которой тело падает изначально. В нашем случае H = S2, а H' = 0 - ведь нас интересует полное время полёта с высоты H = S2, а полное время полёта тела будет таковым тогда, когда тело упадёт, то есть его высота будет равна нулю. Вот и получается, что
H' = H - gt'²/2
0 = S2 - gt2²/2
S2 = gt2²/2
Теперь, если общее время равно t, то оно будет складываться из времени, затраченного на первый путь, и времени, затраченного на второй:
t = t1 + t2
Получается, что мы можем выразить времена t1 и t2 из каждого уравнения и приравнять сумму их выражений к известному времени t. Но проблема в том, что нам неизвестны значения S1 и S2, ведь выражая t1 и t2 справа, слева в уравнении будут находиться S1 и S2, и решить задачу не получится. Значит, надо как-то выразить ещё и пути. Подумаем. Тело подбросили с высоты h = 15 м. Оно поднялось на высоту (h + X), затем стало падать. Поравнявшись с точкой, из которой тело изначально полетело вверх, оно снова оказалось на высоте h. Тогда выходит, что путь тела вверх равен X. А путь тела вниз равен (h + X):
S1 = X
S2 = h + X
Теперь надо подумать, как можно представить этот X.
Так как движение вверх происходит с начальной скоростью, не равной нулю, а тело замедляется по мере подъёма, то в верхней точке эта скорость станет как раз-таки равной нулю. Мы можем найти время, через которое скорость обратится в нуль. Вот уравнение для скорости:
v = v0 - g*t1 (опять же - "минус", потому что g направлено против оси Y)
v = 0 => 0 = v0 - g*t1 => v0 = g*t1
Теперь выразим время из получившегося уравнения:
v0 = g*t1 => t1 = v0/g
Вот, уже получили выражение для t1. Теперь подставим полученное выражение в уравнение для S1:
S1 = v0*t1 - g*t1²/2 = v0*(v0/g) - g*(v0/g)²/2 = v0²/g - v0²/2g = (2v0² - v0²)/2g = v0²/2g
Отлично. Теперь мы знаем, что
S1 = X = v0²/2g
S2 = h + X = h + (v0²/2g)
Получим выражение для t2:
S2 = gt2²/2
h + (v0²/2g) = gt2²/2 | * 2g
2gh + v0² = g²t2²
t2² = (2gh + v0²)/g² => t2 = √((2gh + v0²)/g²)) = √(2gh + v0²)/g
Теперь приравниваем сумму t1 и t2 к t:
t = t1 + t2
t = v0/g + √(2gh + v0²)/g | * g
t*g = v0 + √(2gh + v0²)
t*g - v0 = √(2gh + v0²) | ² - возведём обе части в квадрат
(t*g - v0)² = 2gh + v0²
t²g² - 2tg*v0 + v0² = 2gh + v0² - переносим слагаемое "-2tg*v0" вправо, а всё остальное собираем в левой части:
t²g² + v0² - 2gh - v0² = 2tg*v0
2tg*v0 = t²g² - 2gh | : g
2t*v0 = t²g - 2h - ну вот и всё, остаётся только выразить v0 и найти его значение:
v0 = (t²g - 2h)/2t = (3²*10 - 2*15)/2*3 = (9*10 - 30)/6 = (90 - 30)/6 = 60/6 = 10 м/с
Получается, что тело пролетело вверх
t1 = v0/g = 10/10 = 1 c,
а вниз
S2 = gt2²/2
t2² = S2/(g/2) = 2*S2/g = 2*(h + (v0²/2g))/g = 2*(15 + (10²/2*10))/10 = 2*(15 + (100/20))/10 = 2*(15 + 5)/10 = 2*20/10 = 40/10 = 4
t2² = 4 => t2 = √4 = 2 c
t = t1 + t2 = 1 + 2 = 3
3 = 3 - значит, ответ верный.
Ответ: 10 м/с.