Предмет: Математика,
автор: artmmelnikov1999
Решить этот интеграл с подробным решением
Приложения:
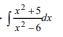
Ответы
Автор ответа:
1
Ответ:
Похожие вопросы
Предмет: Русский язык,
автор: ritaberezkina2
Предмет: Українська література,
автор: Jenova16
Предмет: Русский язык,
автор: Sasha21062003
Предмет: Математика,
автор: Narmina153шк