Предмет: Математика,
автор: Kira4074
Алгебра 8 класс. Задание ниже.
Приложения:
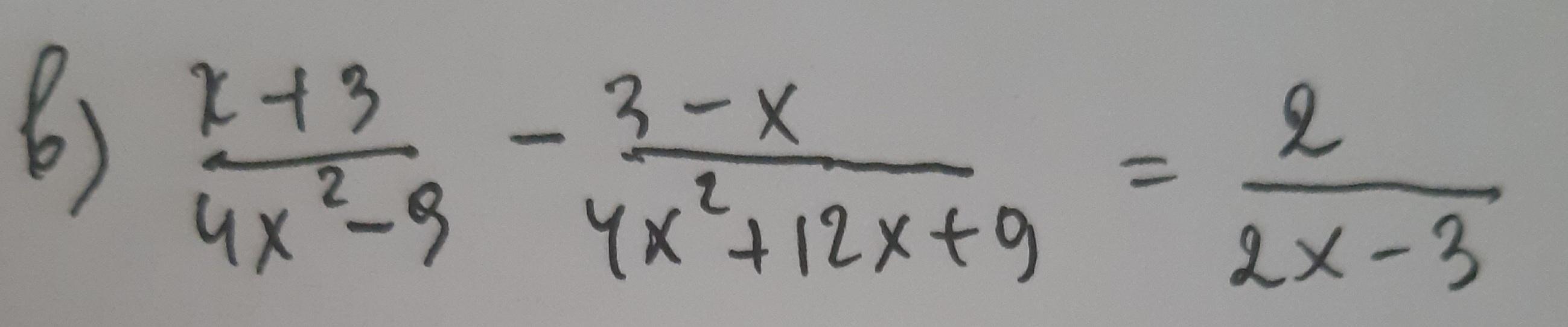
Ответы
Автор ответа:
0
Ответ:
,
Пошаговое объяснение:
Формула разности квадратов -
Формула квадрата суммы -
Похожие вопросы
Предмет: Русский язык,
автор: kcuni2005
Предмет: Русский язык,
автор: dea123
Предмет: Русский язык,
автор: mirzoeva1
Предмет: Алгебра,
автор: russckaiakat
Предмет: История,
автор: nekzard