Предмет: Алгебра,
автор: temavonmazurok777
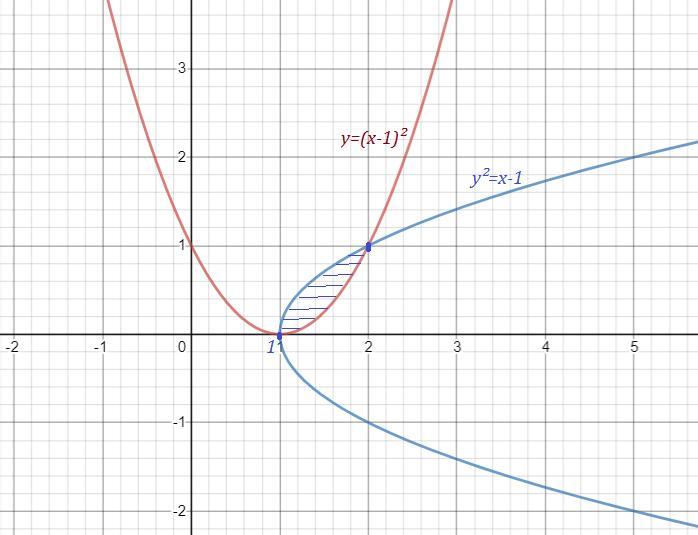
Найти площадь фигуры между функциями с помощью интегралов. Даны две функции: y=(x-1)^2; y^2=(x-1).
Ответы
Автор ответа:
1
Ответ:
Приложения:
Похожие вопросы
Предмет: Английский язык,
автор: Диса1111
Предмет: Русский язык,
автор: Аноним
Предмет: Русский язык,
автор: iiiiiiiiiiiiiiooo
Предмет: Английский язык,
автор: alenabex19751601
Предмет: Математика,
автор: MarinaBabayan50