Предмет: Математика,
автор: oficerovavalenti
Решите пожалуйста.
С подробным решением.
Заранее спасибо.
Приложения:
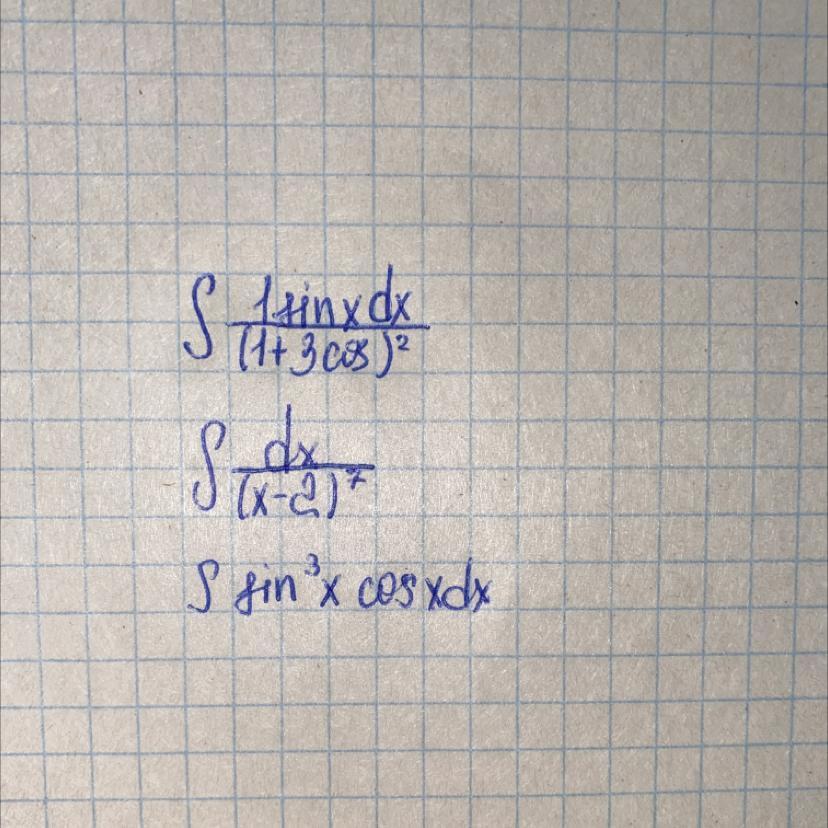
Ответы
Автор ответа:
1
Ответ:
Пошаговое объяснение:
Похожие вопросы
Предмет: Русский язык,
автор: Zarifaaaa
Предмет: Русский язык,
автор: Аноним
Предмет: Другие предметы,
автор: parta551
Предмет: Математика,
автор: Xanteer
Предмет: Математика,
автор: Люба134578