Предмет: Алгебра,
автор: yarik65681
решите уравнение sin X - cos X = корень из 2 если X = [0; pi]
Приложения:
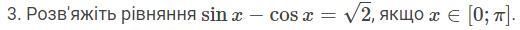
Ответы
Автор ответа:
1
Ответ:
n принадлежит Z.
на [0;П]
Автор ответа:
1
Ответ:
Похожие вопросы
Предмет: Английский язык,
автор: rystam131006
Предмет: Английский язык,
автор: csukhanova2015
Предмет: Английский язык,
автор: 89613269492
Предмет: Английский язык,
автор: PiRoZhEnKa2007