Предмет: Геометрия,
автор: fatsecret31
Висота прямокутного трикутника з гострим кутом а, проведена до гіпотенузи, дорівнює h. Знайдіть гіпотенузу цього трикутника.
Ответы
Автор ответа:
14
Ответ:
Объяснение:
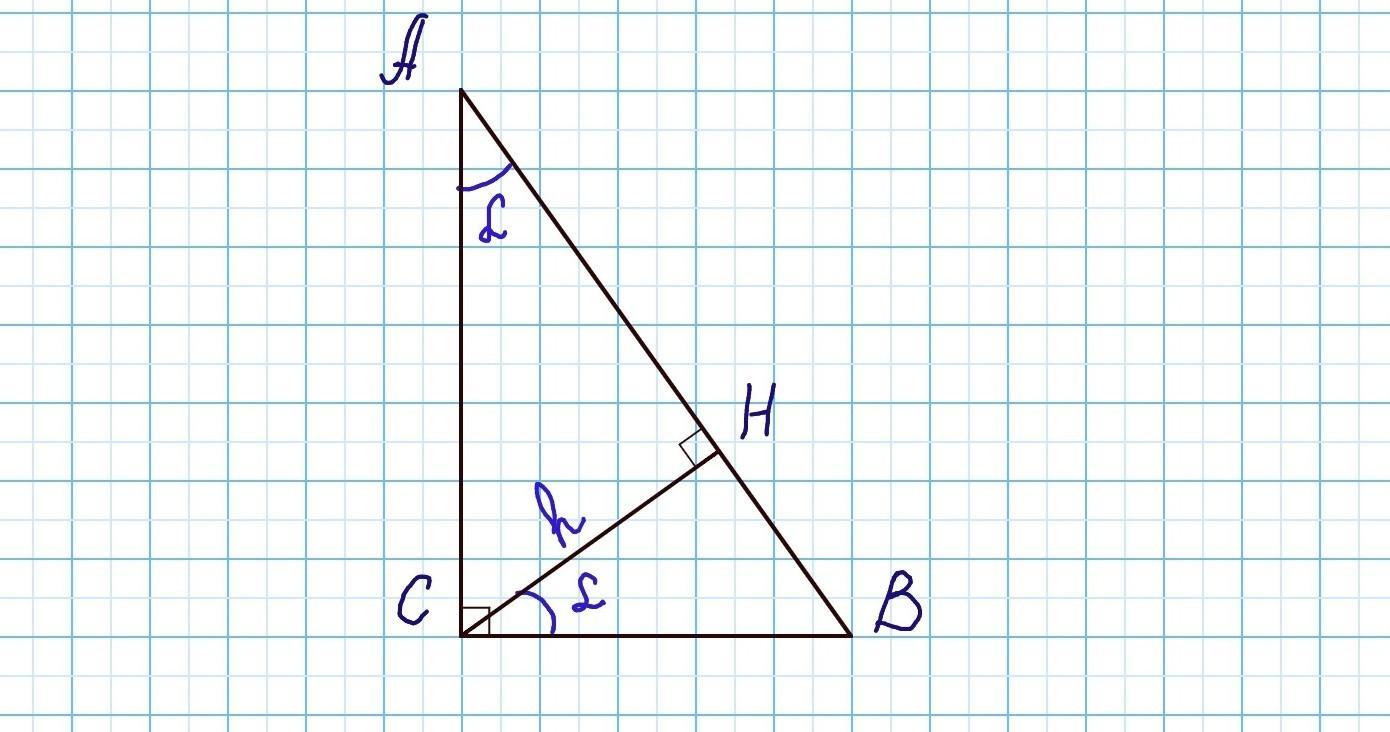
△АВС, ∠С=90°, ∠A=α, СН⟂АВ, СН=h.
АВ-?
1)Рассмотрим прямоугольный треугольник △АНС.
АН=СН×ctg α=h×ctg α
2)Рассмотрим прямоугольный треугольник △НВС.
∠НВС=90°- ∠A=90°-α - по свойству острых углов прямоугольного треугольника. =>
∠НСВ=90°- ∠НВС=90°-(90°-α)= α
НВ=СН×tg α = h×tg α
3) АВ=АН+НВ= h×ctg α + h×tg α = h(ctg α + tg α).
Следовательно гипотенуза АВ будет равна:
Приложения:
Похожие вопросы
Предмет: Английский язык,
автор: anastasiyt22
Предмет: Русский язык,
автор: Лера1986
Предмет: Технология,
автор: ledytcheporova
Предмет: Математика,
автор: задачаРЕШИТЕЗА5МИНУТ
Предмет: История,
автор: Аноним