Предмет: Алгебра,
автор: sashasashgavrilov
ПОМОГИТЕ ПОЖАЛУЙСТА, ДАЮ 100 БАЛЛОВ
Приложения:

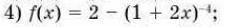

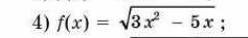
Miroslava227:
производные?
да
Ответы
Автор ответа:
1
Ответ:
1.
2.
3.
4.
спасибо большое )))
Похожие вопросы
Предмет: Русский язык,
автор: kuanaev99
Предмет: Русский язык,
автор: steep6
Предмет: Английский язык,
автор: Аноним
Предмет: Русский язык,
автор: yulya06012015
Предмет: Математика,
автор: swettiikkk