Предмет: Математика,
автор: asmirnow291
Найти площадь трапеции
Приложения:
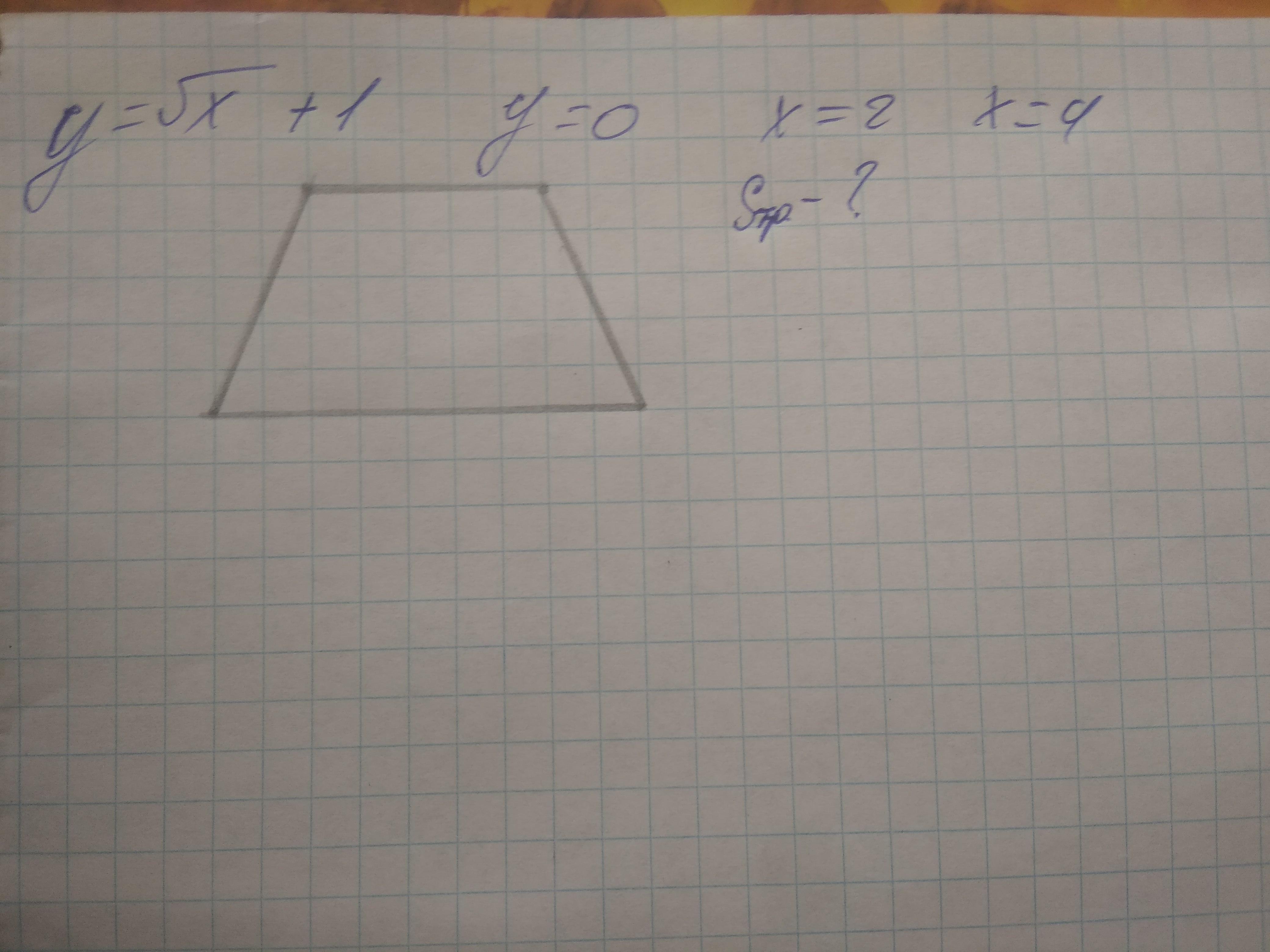
Ответы
Автор ответа:
0
Відповідь:
Покрокове пояснення:
Немного не то, смотрите: когда у нас просят вычислить площадь фигуры (или же трапеции), ограниченной линиями, тогда мы должны использовать формулу Ньютона-Лейбница: - простыми словами, находим интегралы линии, которой ограничена трапеция, a и b - на каком отрезке расположена трапеция.
Сперва в задаче нужно нарисовать графики и прямые на числовой прямой, что указаны в условии: ,
,
,
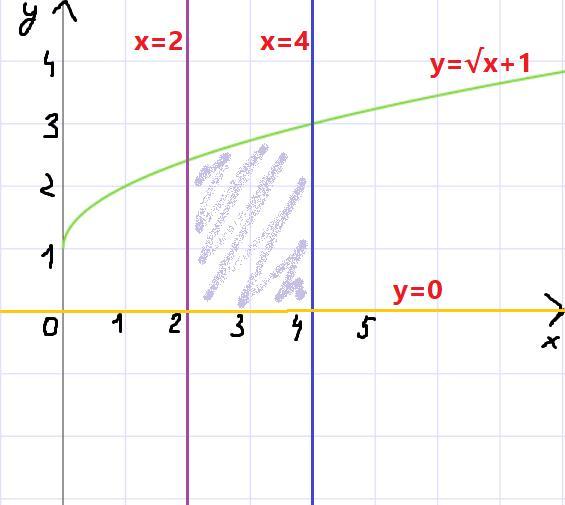
. Примерный график прикрепляю.
Глядя на рисунок, можем сказать, что расположен над осью ОХ, значит можем найти площадь таким образом:
см²
Приложения:
qweqwefifififi:
Если захотите разобрать тему, то это "Вычисление площади фигур с помощью определенного интеграла"
Похожие вопросы
Предмет: Русский язык,
автор: vita7603031844
Предмет: Русский язык,
автор: дашулька47
Предмет: Русский язык,
автор: Кирилл161Ковалев
Предмет: Русский язык,
автор: Simonakka
Предмет: История,
автор: allalis70fchff