Предмет: Алгебра,
автор: Аноним
Помогите умоляю !!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
Приложения:
Polaas:
Помогите пожалуйста очень прошу!
Ответы
Автор ответа:
2
здравствуйте, помогите мне пожалуйста
ответ написала
ёмаё
что это такое а?
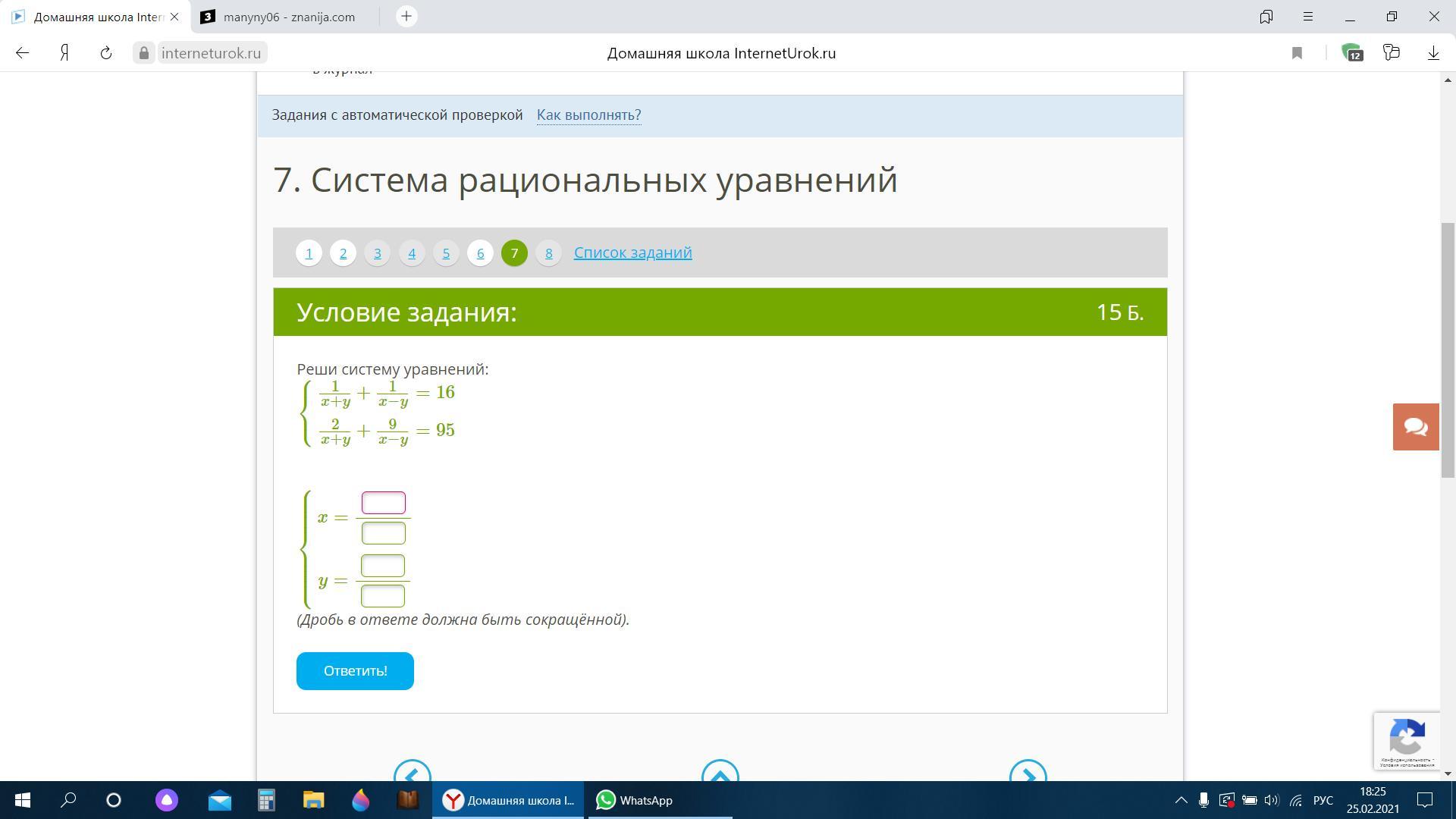
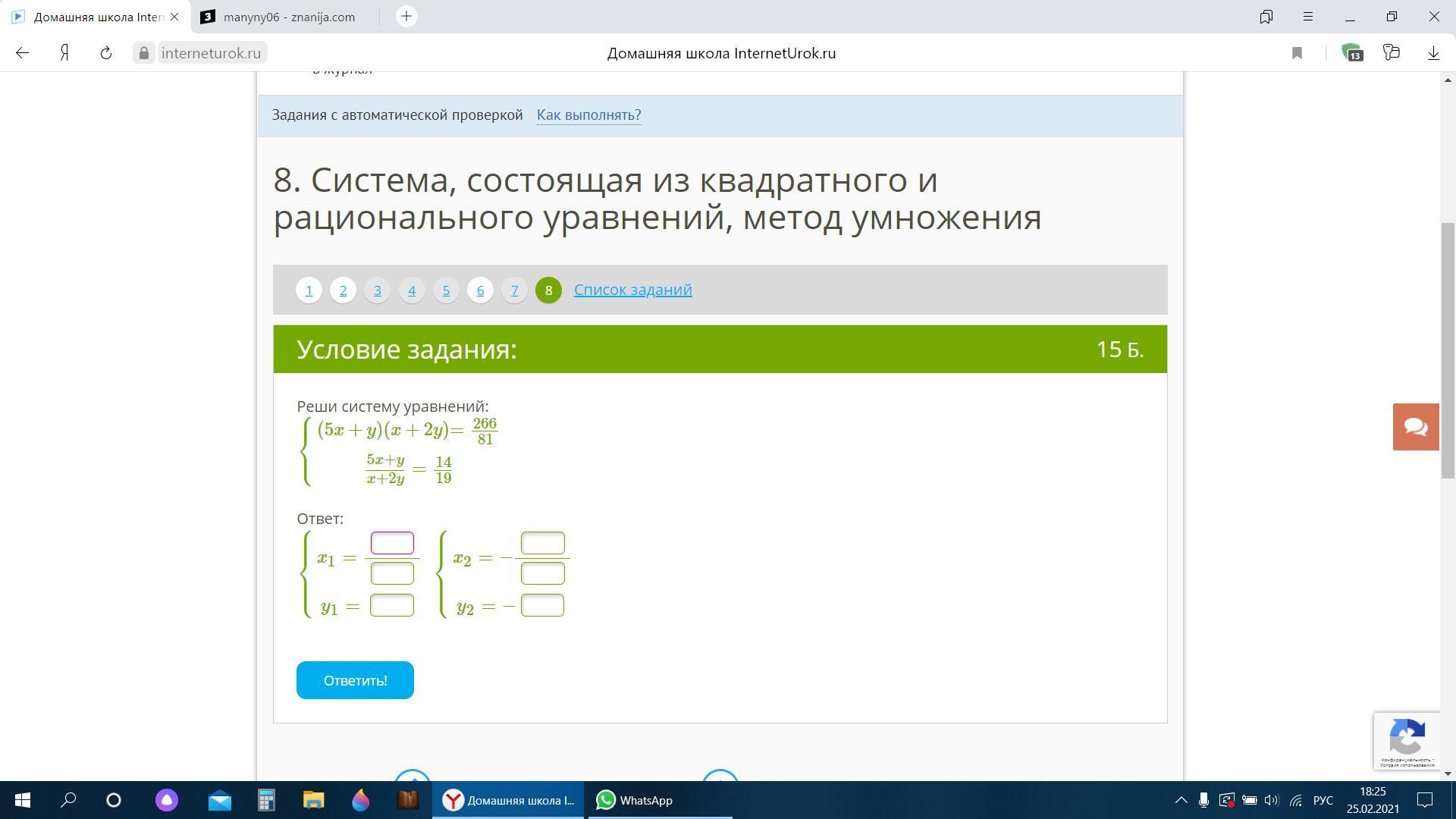
\begin{gathered}1)\ \ \left\{\begin{array}{l}\dfrac{1}{x+y}+\dfrac{1}{x-y}=16\\\dfrac{2}{x+y}+\dfrac{9}{x-y}=95\end{array}\right\ \ \left\{\begin{array}{l}t=\dfrac{1}{x+y}\\p=\dfrac{1}{x-y} \end{array}\right\ \ \left\{\begin{array}{l}t+p=16\\2t+9p=95\end{array}\right\end{gathered}
Это редактор формул, который отображает формулы.... Если тебе не видно, то перезагрузи страницу не с телефона .
прости,,,Пожалуйста
Похожие вопросы
Предмет: Окружающий мир,
автор: sivi1708
Предмет: Окружающий мир,
автор: Ульяна20051
Предмет: Русский язык,
автор: мыктыбек
Предмет: Биология,
автор: veronikakonova
Предмет: Химия,
автор: Александра1701я