Предмет: Геометрия,
автор: nikininatamara
На стороне AC прямоугольного треугольника ABC (угол C — прямой) отмечена точка D. На отрезке BD отмечена точка E так, что BE=AD. Оказалось, что серединные перпендикуляры к отрезкам AB и DE пересекаются на отрезке BC. Найдите длину отрезка BD, если известно, что AD=9, DC=8.
Ответы
Автор ответа:
3
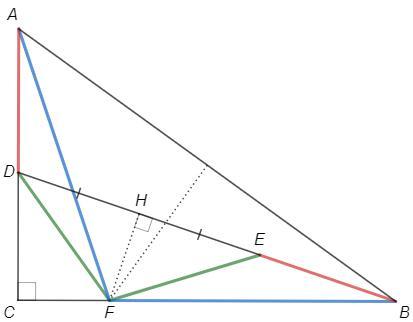
FH - серединный перпендикуляр к DE
Каждая точка серединного перпендикуляра равноудалена от концов отрезка.
FA=FB, FD=FE
△DAF=△EBF (по трем сторонам) => ∠DAF=∠EBF
△BFH=△AFC (по катету и острому углу) => BH=AC => EH=DC
BD =BE+EH+HD =9+8+8 =25
Приложения:
siestarjoki:
△BFH=△AFC по гипотенузе и острому углу
Похожие вопросы
Предмет: Русский язык,
автор: yuliya101
Предмет: Русский язык,
автор: aigasheff
Предмет: Русский язык,
автор: 8080sveta
Предмет: Английский язык,
автор: FILATOV1983
Предмет: Русский язык,
автор: seytalievarman