Предмет: Геометрия,
автор: avasilenko686
Знайдіть центральний кут правильного двадцятикутника
Ответы
Автор ответа:
19
Около любого правильного многоугольника можно описать окружность, центр которой совпадает с центром этого многоугольника. Если у многоугольника n сторон, то центральных углов у него также n и все они равны между собой.
Градусная мера всей окружности — 360º, следовательно, градусная мера каждой дуги окружности, на которую окружность разбивают вершины n-угольника, равна 360/n
Так как центральный угол равен дуге, на которую от опирается, то и каждый из центральных углов равен 360º:n.
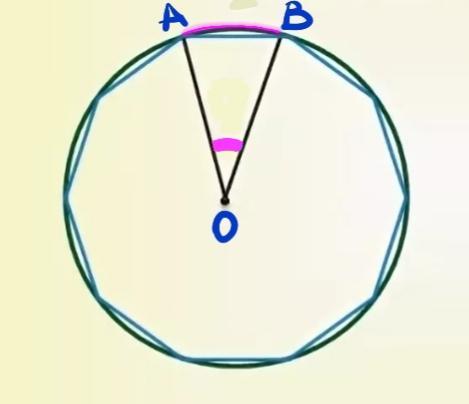
Обозначим центральный угол как < АОВ.
Т.к у нас правильный двадцатиугольник,то центральный угол АОВ равен:
<АОВ = 360: n = 360:20=18°
Дано: <АОВ-центральный угол двадцатиуг-ка, n= 20 .
Найти: <AOB.
Решение:
<AOB= 360÷20=18°
Ответ: 18°
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: atabekyanlilit
Предмет: Английский язык,
автор: fydfhduduf
Предмет: Русский язык,
автор: alevtina86
Предмет: Русский язык,
автор: MarryBlack
Предмет: Английский язык,
автор: mikimays2003Sasha