Предмет: Математика,
автор: Аноним
Помогите решить производную.Пожалуйста!!!!!!!!!!!!!!!!!!!
Приложения:
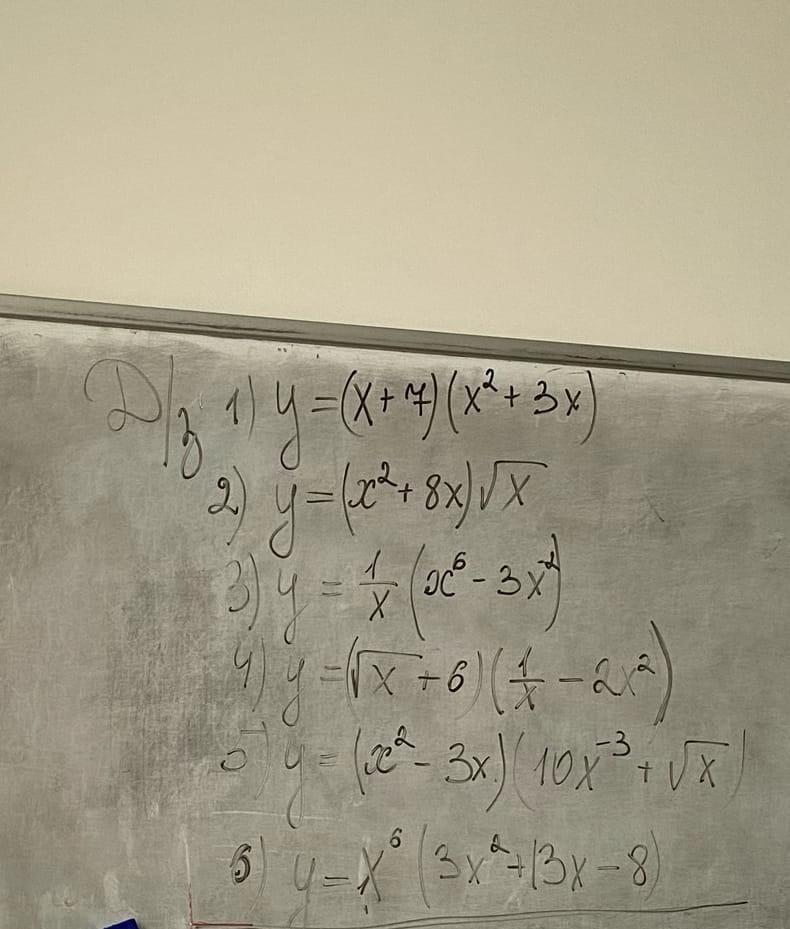
Ответы
Автор ответа:
3
Ответ:
1.
2.
3.
4.
5.
6.
Похожие вопросы
Предмет: Немецкий язык,
автор: 678pj
Предмет: Английский язык,
автор: 79037611259
Предмет: Английский язык,
автор: Kate8975
Предмет: Математика,
автор: 53213
Предмет: Литература,
автор: mdfgc