Question

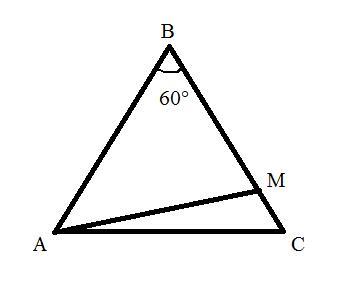
Треугольник АВС - равносторонний, М - внутренняя точка отрезка ВС. Докажите, что АМ<АВ​

Answer 1

Ответ:

Объяснение:

М - внутренняя точка отрезка ВС, значит всегда BM<BC и значит BM<AB. Раз так, то <BAM всегда будет меньше первоначальных 60°, а <BMA наоборот всегда >60° (это очевидно из теоремы "против большей стороны лежит больший угол"). И чем ближе М к B, тем <BAM меньше, а <BMA больше. При этом <ABМ=60° остаётся всегда.

По обратной к предыдущей теореме, против угла <BMA лежит большая сторона, чем против угла <ABM так как <BMA>60°. Значит AM<AB чтд.