Question

просто ответ.
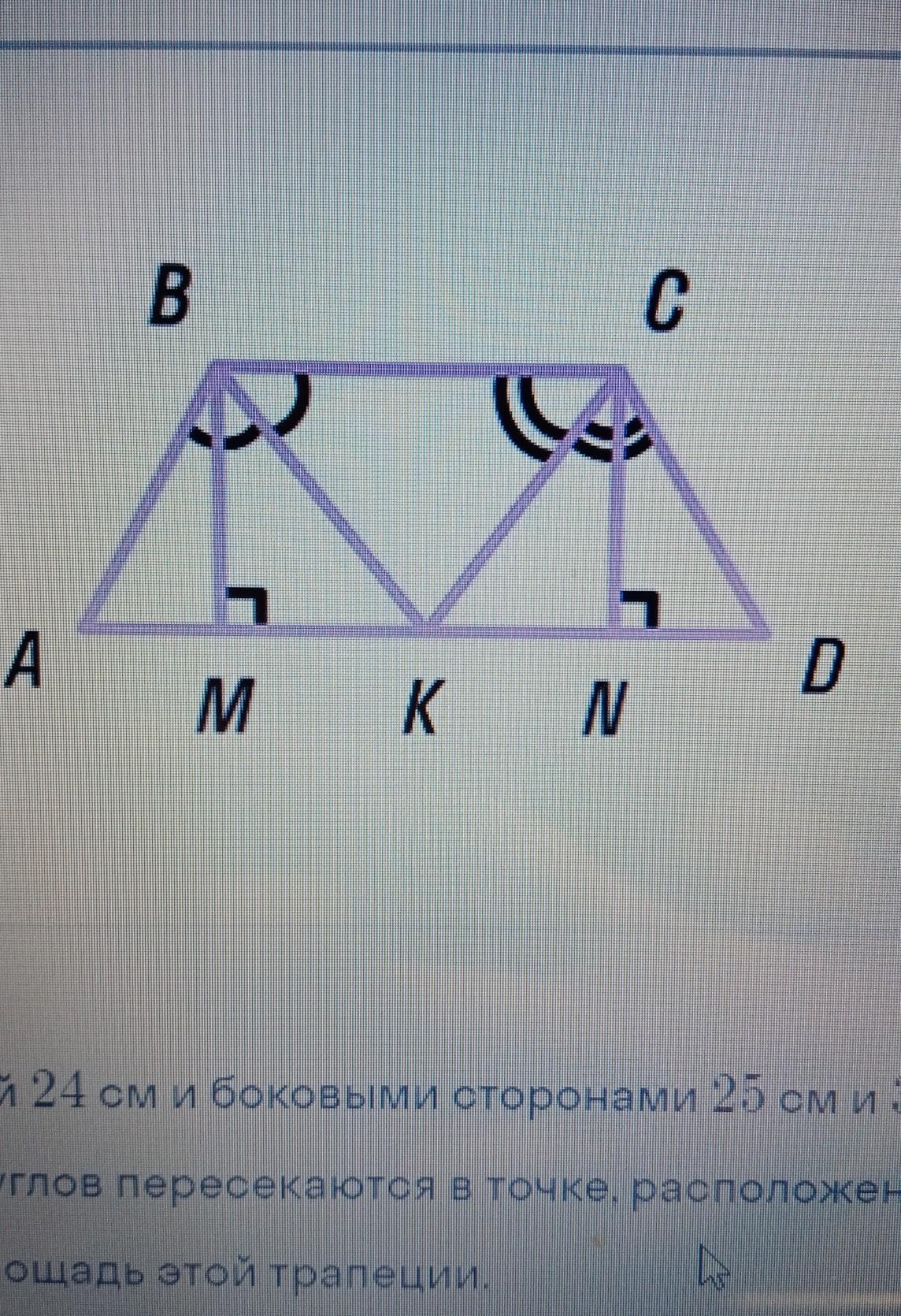
в трапеции с высотой 24см и боковыми сторонами 25 и 30см биссектрисы тупых углов пересекаются в точке, расположенной на большем основании. найди площадь трапеции ​

Answer 1

Ответ:

1020 кв.см

Объяснение:

• Если биссектрисы тупых углов трапеции пересекаются в точке, принадлежащей большему основанию, то большее основание равно сумме боковых сторон трапеции.

Действительно, <КВС=<АКВ - как внутренние накрест лежащие при параллельных прямых ВС и AD и секущей ВК. Но <КВС=<АВК => <АКВ=<АВК, значит треугольник АВК - равнобедренный, а по свойству равнобедренных треугольников имеем равенство боковых сторон: АК=АВ=25 см

Аналогично КD=CD=30 см.

Большая сторона трапеции: AD=AK+KD=25+30=55 см

Рассмотрим прямоугольный треугольник АВМ. По теореме Пифагора найдём катет АМ:

$AM = \sqrt{ {AB}^{2} - {BM}^{2} } =\sqrt{ {25}^{2} - {24}^{2} } = \sqrt{(25 - 24)(25 + 24)} = \sqrt{49} = 7$см

В прямоугольном треугольнике DCN найдём катет ND:

$ND = \sqrt{ {CD}^{2} - {CN}^{2} } = \sqrt{ {30}^{2} - {24}^{2} } = \sqrt{900 - 576} = \sqrt{324} = 18$см

Тогда MN=AD-AM-ND=55-7-18=30 см

Т.к. MBCN - прямоугольник, то меньшее основание трапеции ВС=MN=30 см

Площадь трапеции равно полусумме её оснований умноженное на высоту:

$S = \dfrac{BC + SD}{2} \times BM = \dfrac{30 + 55}{2} \times 24 = 85 \times 12 = 1020$кв см