Question

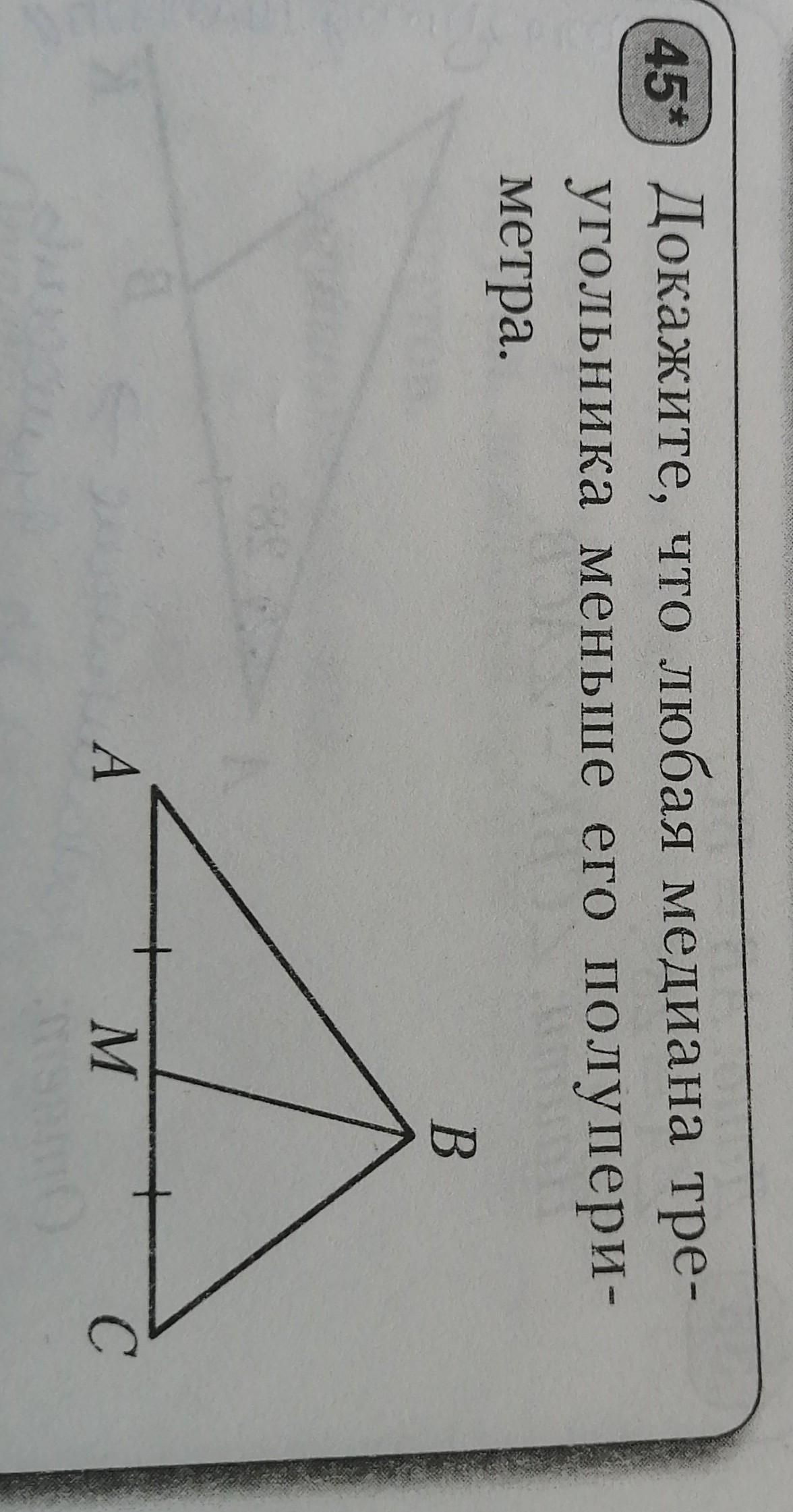
45) Докажите, что любая медиана тре-
угольника меньше его полупери-
метра.
​

Answer 1

Ответ:

Построим произвольный треугольник ABC и его медиану BD.

Мы знаем теорему о том что, одна из сторон треугольника всегда меньше суммы двух других сторон. По этому:

Сложим эти неравенства (cвойство неравенств в арифметике)

Так как DA + DC это AC, то перепишем:

Из неравенства видим, что медиана меньше полупериметра. Таким же образом теорема доказывается для оставшихся двух медиан.