Предмет: Алгебра,
автор: Tekee
Составить уравнение прямой, проходящей через центр кривой второго порядка 4х^2+y^2+16x-2y+15=0 перпендикулярно прямой 2x+y+5=0
Попробовал решить сам,вот что получилось. а что делать дальше. как привести к каноническому виду?
Приложения:
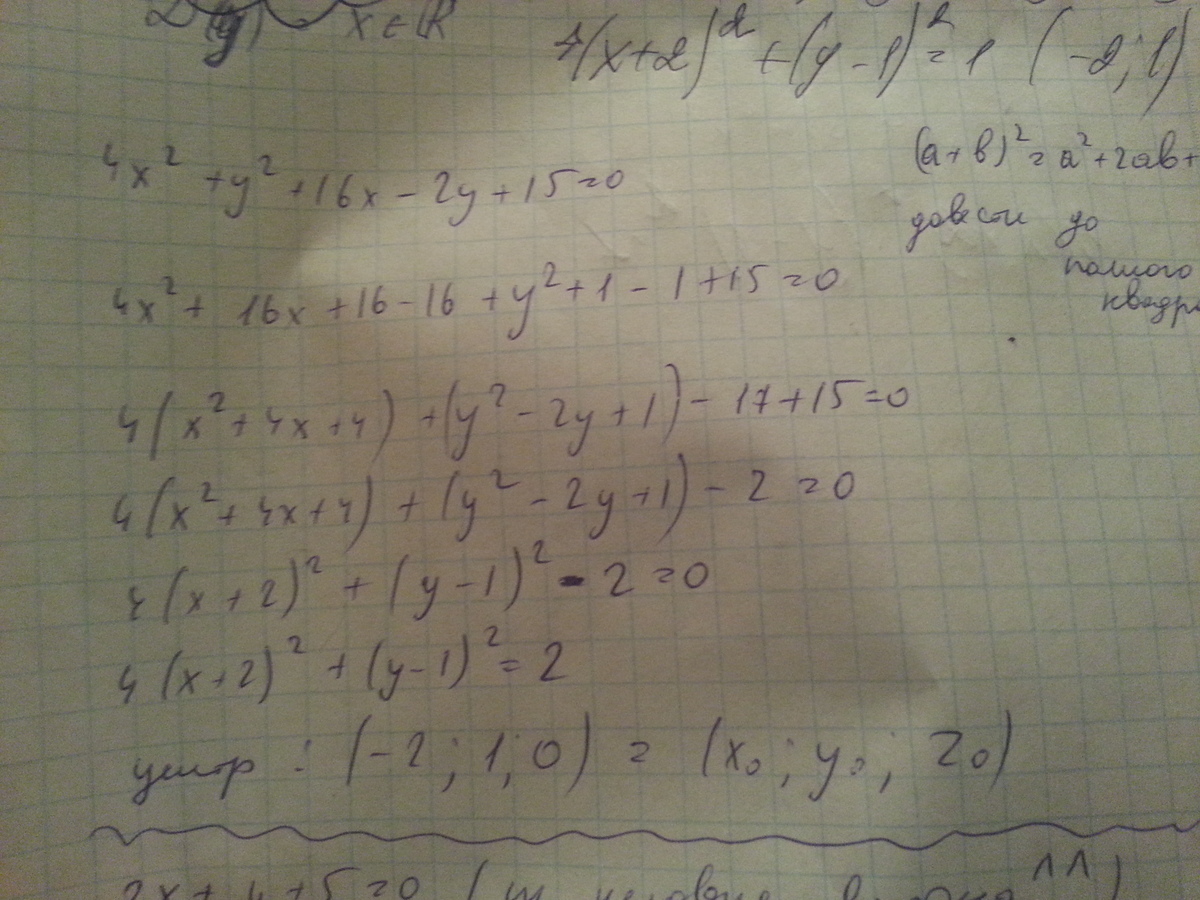
Ответы
Автор ответа:
0
4(x²+4x+4)-16+(y²-2y+1)-1+15=0
4(x+2)²+(y-1)²=2

Центр кривой точка (-2;1)
Данное уравнение прямой запишем как у=-2х-5
ее угловой коэф. k=-2
Так как искомая прямая перпенд. данной, то ее угловой коэф. k1=-1/2. Значит ее уравнение будет у=(-1/2)х+b
Координаты точки (-2;1) должны удовлетворять уравнение искомой прямой, значит: 1=(-1/2)*(-2)+b => b=0
Уравнение прямой: у=(-1/2)х.
4(x+2)²+(y-1)²=2
Центр кривой точка (-2;1)
Данное уравнение прямой запишем как у=-2х-5
ее угловой коэф. k=-2
Так как искомая прямая перпенд. данной, то ее угловой коэф. k1=-1/2. Значит ее уравнение будет у=(-1/2)х+b
Координаты точки (-2;1) должны удовлетворять уравнение искомой прямой, значит: 1=(-1/2)*(-2)+b => b=0
Уравнение прямой: у=(-1/2)х.
Автор ответа:
0
4(x²+4x+4)-16+(y²-2y+1)-1+15=0
4(x+2)²+(y-1)²=2
Центр кривой точка (-2;1)
Данное уравнение прямой запишем как у=-2х-5
ее угловой коэф. k=-2
Так как искомая прямая перпенд. данной, то ее угловой коэф. k1=-1/К. Значит ее уравнение будет у=(1/2)х+b
Координаты точки (-2;1) должны удовлетворять уравнение искомой прямой, значит: 1=(1/2)*(-2)+b => b=2
Уравнение прямой: у=(1/2)х + 2
4(x+2)²+(y-1)²=2
Центр кривой точка (-2;1)
Данное уравнение прямой запишем как у=-2х-5
ее угловой коэф. k=-2
Так как искомая прямая перпенд. данной, то ее угловой коэф. k1=-1/К. Значит ее уравнение будет у=(1/2)х+b
Координаты точки (-2;1) должны удовлетворять уравнение искомой прямой, значит: 1=(1/2)*(-2)+b => b=2
Уравнение прямой: у=(1/2)х + 2
Похожие вопросы
Предмет: Оʻzbek tili,
автор: Аноним
Предмет: Химия,
автор: vraczkayaalena58
Предмет: Математика,
автор: akangazusabina320
Предмет: Биология,
автор: Antonixs
Предмет: Математика,
автор: 2343545