Предмет: Геометрия,
автор: linaaaaaaa3214
Найдите площадь прямоугольной трапеции боковые стороны которой относятся как 4:5 ,а разность оснований равна 9 см если её большая диагональ равна 20 см
Ответы
Автор ответа:
4
Ответ:
138 с
Объяснение:
Трапеция. Основания a, b. Боковые стороны c и d, диагональ е
sin(a) = 4:5 = 0.8. Угол а = 53.13*
с = (a-b)/tg(a) = 9 * 1\frac{1}{3} = 12, теперь находим d:
c : d => 4 : 5 = 12 : x
4x = 60
x = 15
Сторона а: корень из = 20^{2} - 12^{2} = 16
Сторона b: 16 - 9 = 7
Площадь трапеции: с * (a+b) / 2 = 12 * 23 / 2 = 138
Приложения:
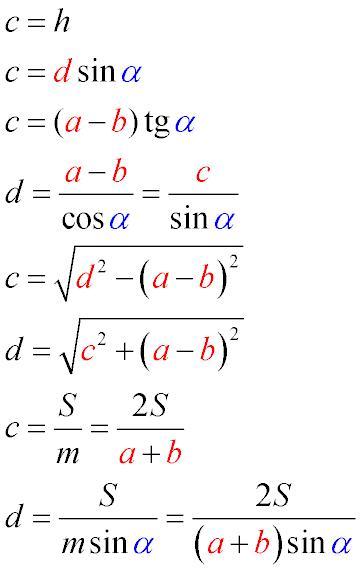
Похожие вопросы
Предмет: Русский язык,
автор: fhhdsh
Предмет: Русский язык,
автор: zenia3
Предмет: Русский язык,
автор: tahminahasan86
Предмет: Русский язык,
автор: анна2382
Предмет: Математика,
автор: AriadnaKat