Предмет: Алгебра,
автор: Сомурская
Помогите решить, очень срочно! Даю много балов !
Приложения:
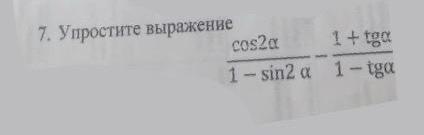
Ответы
Автор ответа:
1
Ответ:
Похожие вопросы
Предмет: Английский язык,
автор: newLife5
Предмет: Английский язык,
автор: aibanuserikovna
Предмет: Русский язык,
автор: Мирай69
Предмет: Русский язык,
автор: Аноним
Предмет: Русский язык,
автор: Дашуля311