Предмет: Алгебра,
автор: malikanurhodjaeva
Напишите первые пять членов последовательности {an}:
Приложения:
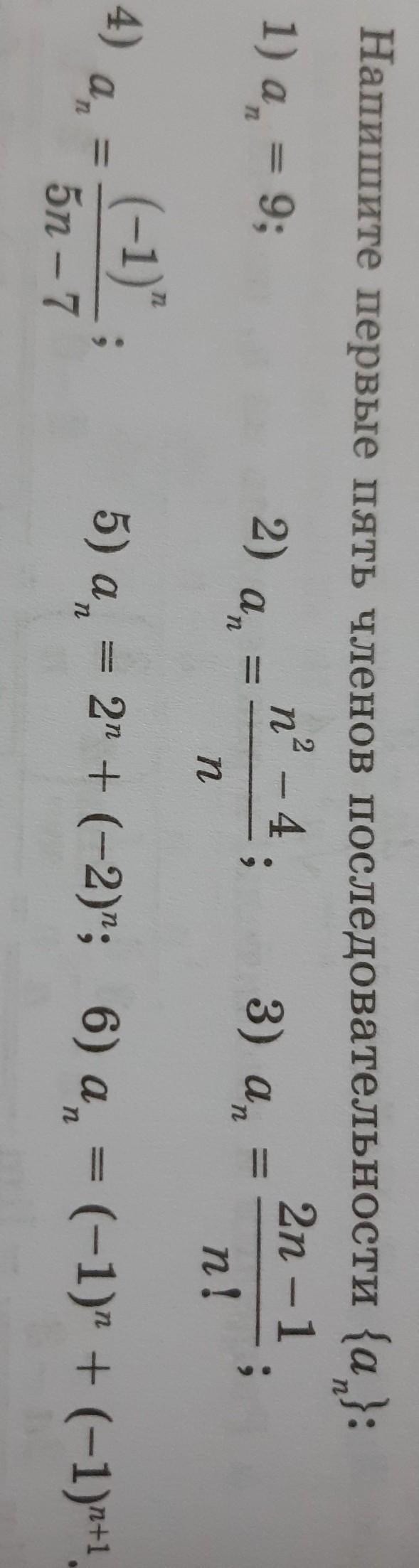
malikanurhodjaeva:
пожалуйста помогите!!!
Ответы
Автор ответа:
1
Объяснение:
Ответ: 9; 9; 9; 9; 9.
Ответ: -3; 0; 1²/₃; 3; 4¹/₅.
Ответ: 1; 3/2; 5/6; 7/26; 3/40.
Ответ: 1/2; 1/3; -1/8; 1/13; -1/18.
Ответ: 0; 8; 0; 32; 0.
Ответ: 0; 0; 0; 0; 0;.
Спасибо огромное.
Удачи.
Похожие вопросы
Предмет: Окружающий мир,
автор: torshinoleg
Предмет: Английский язык,
автор: veraveravera007007
Предмет: Английский язык,
автор: supfire2013
Предмет: Математика,
автор: Арина100406
Предмет: Английский язык,
автор: SizovMarina