Предмет: Геометрия,
автор: ARMYDila
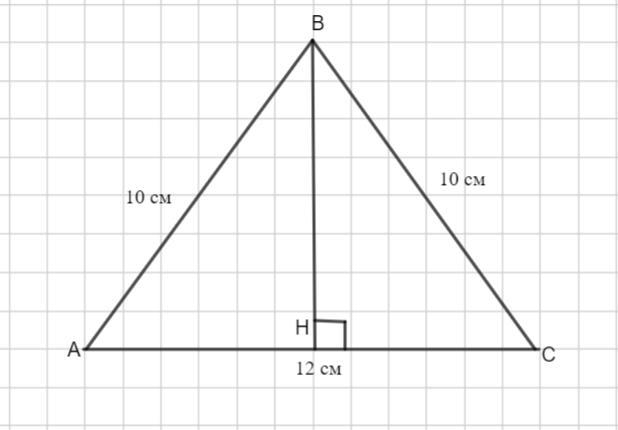
Найди площадь равнобедренного треугольника, если его основание равно 12 см, а боковая сторона равна 10 см.
/ Прикрепи тут фотографию полного канонического решения
Ответы
Автор ответа:
3
Ответ:
Площадь треугольника равна 48 см²
Объяснение:
Рассмотрим треугольник АВС- равнобедренный.
АВ=ВС=10 см, АС= 12 см.
1 способ.
Проведем высоту ВН. В равнобедренном треугольнике она является медианой. Значит, АН=НС= 12:2=6 см.
Рассмотрим треугольник АВН - прямоугольный. Найдем ВН по теореме Пифагора: в прямоугольном треугольнике квадрат гипотенузы равtн сумме квадратов катетов.
Высота BH равна 8 см.
Площадь треугольника найдем по формуле:
где a- сторона треугольника, h- высота, проведенная к ней.
Площадь треугольника равна 48 см².
2 способ.
Найдем площадь треугольника по формуле Герона.
где и
стороны треугольника.
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: ЛюсиRu
Предмет: Русский язык,
автор: rlalacova
Предмет: Русский язык,
автор: дашулик2
Предмет: Английский язык,
автор: Школьник200111
Предмет: История,
автор: mdani23122013p2lhbb