Предмет: Математика,
автор: ayatchenko
Вычислить объем тела вращения вокруг оси Ох фигуры, ограниченной линиями y=2x и y=√x . (Помогите,пожалуйста, решить с кратким объяснением)
Ответы
Автор ответа:
1
Ответ:
см рис
Пошаговое объяснение:
Приложения:
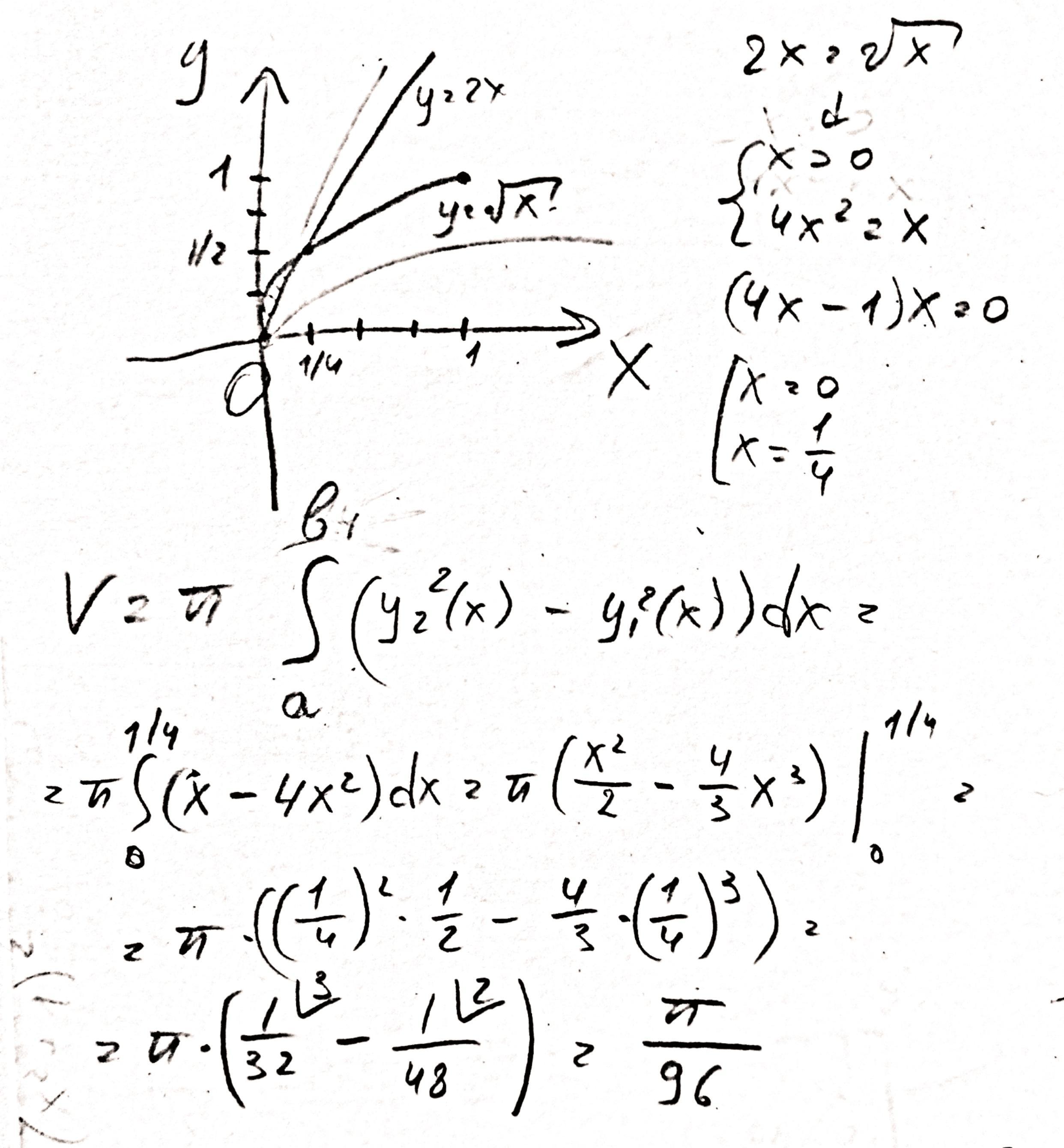
math28929:
помогите пожалуйста с геометрией
срочно
Нужна помощь по геометрии
СРОЧНО!!!
Автор ответа:
2
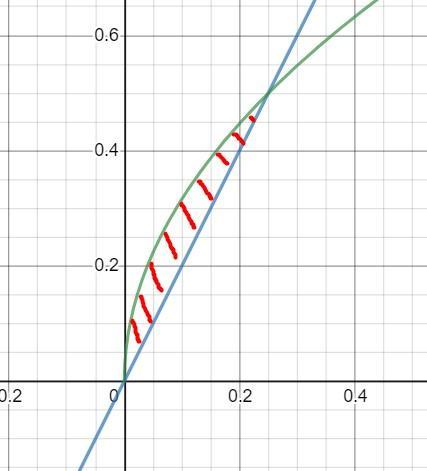
Пошаговое объяснение:
График во вложении.
Найдём точки пересечения линий:
2x=√x
4x²=x
4x²-x=0
x(4x-1)=0
x=0 и x=1/4
Объём тела вращения(найдём как разность объёма верхней и нижней фигуры):
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: юлия1236
Предмет: Русский язык,
автор: bossik1319
Предмет: Другие предметы,
автор: chornaya30
Предмет: Математика,
автор: Валерыч2005
Предмет: Математика,
автор: Lenovo1609201